根据项目反应理论,对考生进行测试的主要目的是在能力量表上定位该人。如果每个参加测试的考生获得这样的能力度量,则可以根据考生拥有多少潜在能力来对其进行评估,比较等。
一、能力 $\theta$ 估计方法
若用于测量潜在特征(latent trait)的测试将由 $J$ 个项目组成,且每个项目都测量该特征的某些方面。为了估计考生的能力$\theta$,假设测试项目的参数已知,进行测试时,考生将对测试中的 $J$ 个项目中的每一个做出回答,并以二分法计分。
根据项目反应理论,采用最大似然法估计考生的能力$\theta$,双参数模型能力估计方程如下:
$$
\hat{\theta}{s+1}=\hat{\theta}{s}-\frac{\sum_{j=1}^{J} a_{j}\left[u_{j}-P_{j}\left(\hat{\theta}{s}\right)\right]}{-\sum{j=1}^{J} a_{j}^{2} P_{j}\left(\hat{\theta}{s}\right) Q{j}\left(\hat{\theta}{s}\right)} \tag1
$$
其中,
$\hat{\theta}_{s}$为考生在第$s$次迭代内的估计能力;
$a_{j}$为项目第$j$个项目的项目区分度参数;
$u_{j}$是考生对项目 $j$ 的回答,正确响应时$u_{j}=1$,错误响应时$u_{j}=0$;
$P_{j}(\hat{\theta}_{s})$是在第$s$次迭代内,给定ICC曲线参数和;
$\hat{\theta_{s}}$是正确响应项目 $j$ 的概率,$Q_{j}(\hat{\theta}_{s})=1-P_{j}(\hat{\theta}_{s})$为做出错误响应的概率。
计算过程:
开始时,根据经验,设置初始值,如$\hat{\theta}_{s} = 1$。在该能力水平下,使用已知项目参数计算测试中每个项目的正确响应概率。然后计算等号右边的第二项(记为$\Delta \hat{\theta}_{s}$), 即 $\hat{\theta}_{s+1}=\hat{\theta}_{s}-\Delta \hat{\theta}_{s}$
假设一个测试包含3个项目,即$J=3$,每个项目参数(双参模型):
$$b_1=-1.0\quad b_2=0.0\quad b_3=1.0 \
a_1=-1.0\quad a_2=1.2\quad a_3=0.8$$
考生的项目反应 $u_1=1, u_2=0, u_3=1$
考生能力的先验估计 $\hat{\theta_{s}}=1.0$。将这些值代入双参模型:
$$P_{j}\left(\hat{\theta}_{s}\right)=\frac{1}{1+\exp \left[-a_{j}\left(\hat{\theta}_{s}-b_{j}\right)\right]}$$
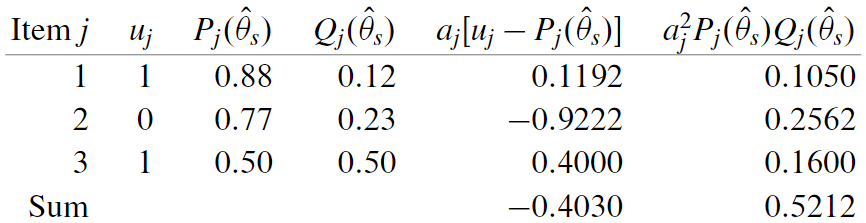
第一次迭代:$\Delta \hat{\theta}_{s}=-0.4030 /(-0.5212)=0.7733,\quad \hat{\theta}_{s+1}=1.0-0.7733=0.2267$
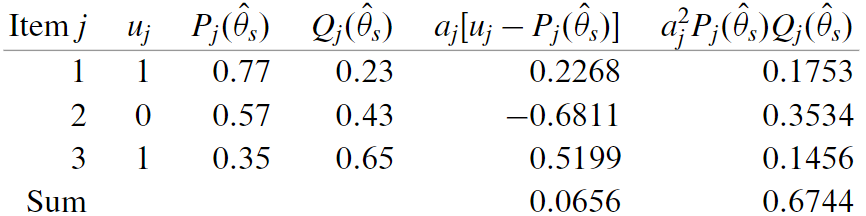
第二次迭代:$\Delta \hat{\theta}_{s}=0.0006 /(-0.6616)=-0.0009, \quad \hat{\theta}_{s+1}=0.3239-(-0.0009)=0.3248$
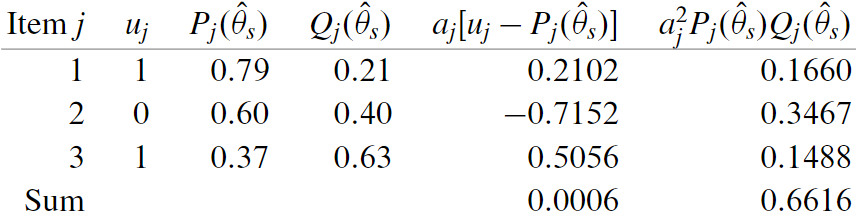
第三次迭代:$\Delta \hat{\theta}_{s}=0.0006 /(-0.6616)=-0.0009, \quad \hat{\theta}_{s+1}=0.3239-(-0.0009)=0.3248$
此时,$\Delta \hat{\theta}_{s}=0.0009$非常小,停止迭代,考生的能力估计值 $\hat{\theta}= 0.32$
考生实际的能力无法计算,只能进行估计,计算其误差。其基本原则是,假设考生可以多次参加相同的考试,且不记得以前的考试项目是如何作答,每次测试获得能力估计为$\hat{\theta}$,考生能力的标准误(standard error):
$$\operatorname{SE}(\hat{\theta})=\frac{1}{\sqrt{\sum_{j=1}^{J} a_{j}^{2} P_{j}(\hat{\theta}) Q_{j}(\hat{\theta})}} \tag2$$
上述例子中,$\mathrm{SE}(\hat{\theta}=0.32)=1 / \sqrt{0.6616}=1.229446$
准误差 1.23 非常大,因此无法非常准确地估计考生的能力。这里主要是因为这里只使用了三个项目。
此外在两种情况下,最大似然法无法产生有效的能力估计。首先,当考生没有答对任何一个项目时,相应的能力估计是负无穷大。二、当一个考生答对所有试题时,对应的能力估计值为正无穷大。在这两种情况下,都不可能获得对考生能力的估计,此情况需要单独处理。
二、考生能力估计的项目不变性 Item Invariance of an Examinee’s Ability Estimate
ICC曲线能横跨整个能力尺度,且能力量表的任意一个子区间都可以用于项目参数估计(项参数的组不变性),ICC曲线的对应段都可用来估计一个考生的能力。因此,在IRT中考生的能力相对于用来测量它的项目是固定不变的,即考生能力估计的项目不变性( Item Invariance of an Examinee’s Ability Estimate)。但需注意,其不变性要满足两个条件: 所有项目都测量相同的潜在特征;所有项目参数使用公共度量(common metric)。
由于考生能力估计的项目不变性,位于能力量表上任何位置的测试都可以用来估计应试者的能力,考生参加“简单”或“困难”的考试,都能获得相同的能力估计。而在经典考试理论中,考生会在简单的考试中获得高分,在困难的考试中得低分,无法确定考生的潜在能力。
需注意“能力固定不变”中关于“固定”一词的含义。考生的能力只有在特定情境下,且具有特定价值的情况下才是固定的。例如,一个考生多次参加同一个测试,只有假定考生不记得这些测试的作答时,能力才是“固定”的。但是,若考生在两次测试之间接受了辅导能力进步,或存在遗留效应,那么在每次测试中考生的潜在能力水平都会有所不同。
考生能力的项目不变性和项目参数的组不变性是IRT不变性原理的两个方面,该原理是IRT的许多实际应用的基础。
三、R语言示例
1. 能力估计过程
前述计算过程R语言实现。
假设一次测验中包含3个,且项目参数(双参)已知。
# 示例
u <- c(1, 0, 1) # 考生作答
b <- c(-1.0, 0.0, 1.0) # 项目难度
a <- c(1.0, 1.2, 0.8) # 项目区分度
th <- 1.0 # 初始能力
J <- length(b) # 项目数
S <- 10 # 迭代次数
ccrit <- 0.001 # 迭代收敛
for (s in 1:S) {
sumnum <- 0.0
sumdem <- 0.0
# 公式1 迭代计算theta
for (j in 1:J) {
phat <- 1 / (1 + exp(-a[j] * (th - b[j])))
sumnum <- sumnum + a[j] * (u[j] - phat)
sumdem <- sumdem - a[j]**2 * phat * (1.0 - phat)
}
delta <- sumnum / sumdem
th <- th - delta
cat(paste("th=", th, "\n"))
if (abs(delta) < ccrit | s == S) {
se <- 1 / sqrt(-sumdem) # 公式2 计算标准差
cat(paste("se=", se, "\n"))
break
}
}
th # 能力
se # 标准差2. 能力参数估计R函数
R 函数估计能力参数,并计算标准误差。
- ablility(mdl, u, b, a, c)
- md1: 模型类别
- u: 考生作答情况(二分计分 0,1)
- b: 各项目难度向量
- a: 各项目区分度向量
- c: 各项目猜对概率向量
ability <- function(mdl, u, b, a, c) {
J <- length(b)
if (mdl == 1 | mdl == 2 | missing(c)) {
c <- rep(0, J)
}
if (mdl == 1 | missing(a)) { a <- rep(1, J) }
x <- sum(u)
# 处理作答全对或全错情况,无标准的普遍方案
# 还可采用 -log(2J-1) log(2J-1)
if (x == 0) {
th <- -log(2 * J)
}
if (x == J) {
th <- log(2 * J)
}
if (x == 0 | x == J) {
sumdem <- 0.0
for (j in 1:J) {
pstar <- 1 / (1 + exp(-a[j] * (th - b[j])))
phat <- c[j] + (1.0 - c[j]) * pstar
sumdem <- sumdem - a[j]**2 * phat * (1.0 - phat) *
(pstar / phat)**2
}
se <- 1 / sqrt(-sumdem)
}
if (x != 0 & x != J) {
th <- log(x / (J - x)) # 能力值初始化
S <- 10
ccrit <- 0.001
for (s in 1:S) {
sumnum <- 0.0
sumdem <- 0.0
for (j in 1:J) {
pstar <- 1 / (1 + exp(-a[j] * (th - b[j])))
phat <- c[j] + (1.0 - c[j]) * pstar
# 能力估计方程,当为单或双参模型时pstar=phat,即为公式1)
sumnum <- sumnum + a[j] * (u[j] - phat) *
(pstar / phat)
sumdem <- sumdem - a[j]**2 * phat * (1.0 - phat) *
(pstar / phat)**2
}
delta <- sumnum / sumdem
th <- th - delta
if (abs(delta) < ccrit | s == S) {
se <- 1 / sqrt(-sumdem)
break
}
}
}
cat(paste("th=", th, "\n")); flush.console()
cat(paste("se=", se, "\n")); flush.console()
thse <- c(th, se)
return(thse)
}
u <- c(1, 0, 1)
b <- c(-1.0, 0.0, 1.0)
a <- c(1.0, 1.2, 0.8)
ability(2, u, b, a)3. 能力估计的抽样变异性
下例用于说明当同一测试进行多次时,考生的能力估计的抽样变异性。
假设模型、项目参数和能力参数已知。
mdl <- 2
theta <- 0.5 # 随机给定一个能力值 rnorm(1, 0, 1)
b <- c(-0.5, -0.25, 0.0, 0.25, 0.5)
a <- c(1.0, 1.5, 0.7, 0.6, 1.8) # 同一测验,且项目参数b,a已知
J <- length(b)
if (mdl == 1 | mdl == 2) { c <- rep(0, J) }
if (mdl == 1) { a <- rep(1, J) }
sumdemt <- 0.0
for (j in 1:J) {
Pstar <- 1 / (1 + exp(-a[j] * (theta - b[j])))
P <- c[j] + (1 - c[j]) * Pstar
sumdemt <- sumdemt - a[j]**2 * P * (1.0 - P) *
(Pstar / P)**2
}
set <- 1 / sqrt(-sumdemt) # 理论标准误
# 测试10次,假定考生不记得每一次作答
R <- 10
thr <- rep(0, R) # 重复测试的能力估计
ser <- rep(0, R) # 重复测试的标准误
for (r in 1:R) {
u <- rep(0, J)
# 根据参数随机生成项目响应向量
for (j in 1:J) {
P <- c[j] + (1 - c[j]) /
(1 + exp(-a[j] * (theta - b[j])))
u[j] <- rbinom(1, 1, P)
}
thse <- ability(mdl, u, b, a, c) # 能力参数估计ablility()函数
thr[r] <- thse[1]
ser[r] <- thse[2]
}
theta # 实际能力
set # 理论标准误
thr
mean(thr)
ser
mean(ser) 4. 考生能力的项目不变性
对给定的考生进行多次不同的测试,能力估计应该集中在考生实际能力附近。
假设考生实际能力参数和测试项目数已知,每个项目参数随机生成,并利用这些参数生成项目响应向量。
mdl <- 2
theta <- 0.5
J <- 30
R <- 10 # 模拟测试次数
thr <- rep(0, R)
ser <- rep(0, R)
for (r in 1:R) {
# 随机项目参数
# b <- round(runif(J,-3,3), 2)
# a <- round(runif(J,0.2,2.8), 2)
# c <- round(runif(J,0,.35), 2)
b <- rnorm(J, 0, 1)
a <- rlnorm(J, 0, 0.25)
c <- rbeta(J, 401, 1601)
if (mdl == 1 | mdl == 2) { c <- rep(0, J) }
if (mdl == 1) { a <- rep(1, J) }
# 根据项目参数模拟项目响应向量
u <- rep(0, J)
for (j in 1:J) {
P <- c[j] + (1 - c[j]) /
(1 + exp(-a[j] * (theta - b[j])))
u[j] <- rbinom(1, 1, P)
}
thse <- ability(mdl, u, b, a, c)
thr[r] <- thse[1]
ser[r] <- thse[2]
}
theta
thr
mean(thr) # 此值接近theta