隐马尔可夫模型(HMM)（二）

HMM 学习问题：
已知观测序列$O＝(o_1，o_2,\cdots,o_T)$，估计模型$\lambda=(A, B, \pi)$参数，使得在该模型下观测序列概率$P(O|\lambda)$最大。

一、监督学习方法

假设已给训练数据包含 $S$个长度相同的观测序列和对应的状态序列 ${ (O_1,I_1), (O_2,I_2), \cdots, (O_S,I_S) }$，那么可以利用极大似然估计来估计隐马尔科夫模型的参数。

转移概率 $a_{ij}$的估计：
设样本中时刻 $t$ 处于状态 $i$ 时刻 $t+1$ 转移到状态 $j$ 的频数为 $A_{ij}$，那么状态转移概率 $a_{ij}$ 的估计是
$$
\hat a_{ij} = \frac{A_{ij}}{\sum_{j=1}^{N}A_{ij}}, \ i=1,2,\cdots,N; \ j = 1,2,\cdots,N
$$
观测概率 $b_j(k)$的估计
设样本中状态为 $j$ 并观测为 $k$ 的频数为 $B_{jk}$，那么状态为 $j$ 观测为 $k$ 的概率 $b_j(k)$的估计是
$$
\hat b_j(k) = \frac{B_{jk}}{\sum_{k=1}^{M}B_{jk}}, \ j=1,2,\cdots,N; \ k = 1,2,\cdots, M
$$
初始状态概率 $\pi_i$ 的估计
$\hat \pi_i$为 $S$个样本中初始状态为 $q_i$的频率。

R示例：HMM参数监督学习

# 模拟参数A，B, Pi
hmm_sim_param <- function(Q,V){
  N <- length(Q) 
  M <- length(V)
  params <- list(
    A = matrix(nrow = N,ncol = N),
    B = matrix(nrow = N,ncol = M ),
    Pi = c(),
    N = N, M=M)

  for (i in 1:N) {  
    temp <- runif(N,0,100)
    Sum <- sum(temp)
    for (j in 1:N) {
      params$A[i,j] = temp[j]/Sum  # 每行参数和为1
    }
  }

  for (i in 1:N) {
    temp <- runif(M,0,100)
    Sum <- sum(temp)
    for (j in 1:M) {
      params$B[i,j] = temp[j]/Sum
    }
  }

  temp <- runif(N,0,100)
  Sum <- sum(temp)
  params$Pi = temp/Sum
  return(params)
}
# 模拟实验数据
hmm_sim_data <- function(n,len){
  gen_data <- function(len = len){
       #随机抽样
    temp_I <- sample(Q,1,replace = T,prob = params$Pi)
    I <- c(temp_I)
    temp_O <- sample(V,1,replace = T,prob = params$B[temp_I,])
    O <- c(temp_O)

    for (i in 2:len) {
      temp_I  <- sample(Q,1,replace = T,prob = params$A[temp_I,])
      I <- c(I,temp_I)
    }

    for (i in 2:len) {
      temp_O <- sample(V,1,replace = T,prob = params$B[I[i],])
      O <- c(O,temp_O)
    }
    return(list(I = I,O = O))
  }

  sim_data <- list()
  for (x in 1:n) {
    sim_data[[x]] <- gen_data(len = len)
  }
  return(sim_data)
}

# 监督学习法
# A
estimate_aij <- function(t,i,j){
  t_i <- sapply(sim_data, function(x){return(x[["I"]][t]==i)})
  next_j <- sapply(sim_data, function(x){return(x[["I"]][t+1]==j)})
  i_j <- sum(t_i & next_j)

  sum_ij <- 0
  for (q in Q) {
    next_q <- sapply(sim_data, function(x){return(x[["I"]][t+1]==q)})
    sum_ij <- sum_ij + sum(t_i & next_q) 
  }

  a_ij <- i_j/sum_ij
  return(a_ij)
}
estimate_A <- function(t=2){
  est_A <-  matrix(nrow = params$N,ncol = params$N)

  for (i in 1:params$N) {
    for (j in 1:params$N) {
      est_A[i,j] <- estimate_aij(t=t,i=i,j=j)
    }
  }
  print("A实际参数：")
  print(params$A)
  print("A估计参数：")
  print(est_A)
  return(est_A)
}
# B
estimate_bjk <- function(j,k){
  j_k <- sapply(sim_data, function(x){
    return(sum(x$I == j & x$O == V[k]))
  })
  b_jk <- sum(j_k)

  sum_jk <- 0
  for (k in 1:params$M) {
    tmp_j_k <- sapply(sim_data, function(x){
      return(sum(x$I == j & x$O == V[k]))
    })
    sum_jk <- sum_jk+sum(tmp_j_k)
  }

  return(b_jk/sum_jk)
}
estimate_B <- function(){
  est_B <-  matrix(nrow = params$N,ncol = params$M)
  for (j in 1:params$N) {
    for (k in 1:params$M) {
      est_B[j,k] <- estimate_bjk(j=j,k=k)
    }
  }
  print("B实际参数：")
  print(params$B)
  print("B估计参数：")
  print(est_B)
  return(est_B)
}
# Pi
estimate_Pi <- function(){
  t_1 <- sapply(sim_data, function(x){
    x[['I']][1]
  })
  freq_t_1 <- table(t_1 )
  est_Pi <- as.vector(prop.table(freq_t_1 ))
  print("Pi实际参数：")
  print(params$Pi)
  print("Pi估计参数：")
  print(est_Pi)
  return(est_Pi)
}

# main
set.seed(1)
Q <- c(1,2,3) # 可能状态集合
V <- c("R","W") # 可能观测集合

params <- hmm_sim_param(Q = Q,V = V)
sim_data <- hmm_sim_data(params,n=1000,len = 10)

est_A <- estimate_A()
est_B <- estimate_B()
est_Pi <- estimate_Pi()

二、无监督学习（Baum-Welch 算法）

无监督学习即用极大似然估计的方法估计参数。Baum-Welch算法，也就是EM算法可以高效地对隐马尔可夫模型进行训练。它是一种非监督学习算法。

假设给定数据只包含了 $S$ 个长度为 $T$ 的观测序列 ${ O_1, O_2, \cdots, O_S }$而没有对应的状态序列，目标是学习隐马尔科夫模型 $\lambda = (A,B,\pi)$的参数。将观测是序列数据看作观测数据 $O$，状态序列数据看作不可观测的隐数据 $I$，那么 HMM 事实上是一个含隐变量的概率模型。
$$
P(O|\lambda) = \sum_{I}P(O|I,\lambda)P(I|\lambda)
$$
其参数学习可以由 EM 算法实现。

Baum-Welch 模型参数估计

输入：观测数据$O=(o_1,o_2,\cdots,o_T)$
输出：HMM模型参数
（1）初始化。对$n=0$, 取$a_{ij}^{(0)},b_{j}(k)^{(0)},\pi_i^{(0)}$, 得到模型$\lambda^{(0)} =(A^{(0)},B^{(0)},\pi^{(0)})$
（2）递推。对$n=1,2,\cdots$
$$
a_{ij}^{(n+1)} = \frac{\sum_{t=1}^{T-1}\xi_t(i,j)}{\sum_{t=1}^{T-1}\gamma_t(i)}
$$

$$
b_j(k)^{(n+1)} = \frac{\sum_{t=1,o_t = v_k}^{T}\gamma_t(j)}{\sum_{t=1}^{T}\gamma_t(j)}
$$

$$
\pi_i^{(n+1)} = \gamma_1(i)
$$
右端各值按观测$O=(o_1,o_2,\cdots,o_T)$和模型$\lambda^{(n)} =(A^{(n)},B^{(n)},\pi^{(n)})$计算。
（3）终止。得到模型参数$\lambda^{(n+1)}$

其中，利用前向概率和后向概率， $\gamma_t(i), \xi_t(i,j)$由下公式给出。

给定模型 $\lambda$ 和观测 $O$，在时刻 $t$ 处于状态$q_i$ 的概率，由前向概率$\alpha_t(i)$和后向概率$\beta_t(i)$定义，记：
$$
\gamma_t(i)=P(i_t=q_i|O, \lambda) = \frac{P(i_t=q_i,O| \lambda)}{P(\lambda|O)}=\frac{\alpha_t(i)\beta_t(i) }{\sum_{j=1}^N{\alpha_t(j)\beta_t(j)}}
$$
给定模型 $\lambda$ 和观测 $O$，在时刻 $t$ 处于状态 $q_i$，且在时刻 $t+1$处于状态 $q_j$ 的概率,记：
$$
\begin{aligned}
\xi_t(i,j)&=P(i_t=q_i,i_{t+1}=q_j|O, \lambda) \\
&= \frac{P(i_t=q_i,i_{t+1}=q_j,O| \lambda)}{P(O|\lambda)}\\
&= \frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{\sum_{i=1}^N\sum_{j=1}^N{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}} \\
\end{aligned}
$$

$\gamma_t(i)$和$\xi_t(i,j)$对各个时刻 $t$ 求和，可以得到一些有用的期望值。

在观测$O$下状态$i$出现的期望值:
$$\sum_{t=1}^T\gamma_t(i)$$
在观测$O$下状态$i$转移的期望值:
$$\sum_{t=1}^{T-1}\gamma_t(i)$$
在观测$O$下由状态$i$转移到状态$j$的期望值:
$$\sum_{t=1}^{T-1}\xi_t(i,j)$$

R示例：Baum-Welch 模型估计HMM参数

gamma <- function(alpha,beta,i,t,N){
  numerator <- alpha[[t]][i]*beta[[t]][i]
  denominator <- 0
  for (j in 1:N) {
    denominator <- denominator+ alpha[[t]][j]*beta[[t]][j]
  }
  return(numerator/denominator)
}

ksi <- function(A,B,alpha,beta,i,j,t,N){
  numerator <- alpha[[t]][i]*A[i,j]*B[j,O[t+1]]*beta[[t+1]][j]
  denominator  <-  0
  for (i in 1:N) {
    for (j in 1:N) {
      denominator <- denominator+alpha[[t]][i]*A[i,j]*B[j,O[t+1]]*beta[[t+1]][j]
    }
  }
  return(numerator/denominator) 
}

forward <- function(A,B,Pi,T_){
  alpha <- list()
  for (t in 1:T_) { 
    if (t == 1) {
      alpha[[t]] <- Pi * B[,O[t]]
    } else {
      alpha[[t]] <- colSums(alpha[[t-1]] * A) * B[,O[t]]
    }
  }
  return(alpha)
}

backward <- function(A,B,N,T_){
  beta <- list()
  for (t in T_:1) { 
    if (t == T_) {
      beta[[t]] <- rep(1,N)
    } else {
      beta[[t]] <- colSums(t(A) * B[,O[t+1]]*beta[[t+1]])
    }
  }
  return(beta)
}

hmm_train <- function(params,O,Q,V){
  A <- params$A
  B <- params$B
  Pi <- params$Pi
  # N状态数 M观测数 T_时刻数
  N <- length(Q)
  M <- length(V)
  T_ <- length(O)

  tmp_A <- matrix(0,nrow = N,ncol = N)
  tmp_B <- matrix(0,nrow = N,ncol = M,dimnames = list(Q,V))
  tmp_Pi <- rep(0,N)

  alpha <- forward(A,B,Pi,T_)
  beta <- backward(A,B,N,T_)

  # a_ij
  for (i in 1:N) {
    for (j in 1:N) {
      numerator <- 0
      denominator  <-  0
      for (t in 1:(T_-1)) {
        numerator <- numerator+ksi(A,B,alpha,beta,i,j,t,N)
        denominator <- denominator+gamma(alpha,beta,i,t,N)
      }
      tmp_A[i,j] <- numerator/denominator
    }
  }

  #b_jk
  for (j in 1:N) {
    for (k in 1:M) {
      numerator <- 0
      denominator  <-  0
      for (t in 1:T_) {
        if (V[k] == O[t]) {
          numerator <- numerator+gamma(alpha,beta,j,t,N)
        }
        denominator <- denominator+gamma(alpha,beta,j,t,N)
      }

      tmp_B[j,k] <- numerator/denominator
    }
  }

  #pi
  for (i in 1:N) {
    tmp_Pi[i] <- gamma(alpha,beta,i,1,N)
  }

  params$A <- tmp_A
  params$B <- tmp_B
  params$Pi <- tmp_Pi
  return(params)
}

hmm_run <- function(params,O,Q,V,maxIter=100,criterion=10e-6){
  for (n in 1:maxIter) {
    old_params <- params
    params <- hmm_train(params,O,Q,V)
    delta_A <- max(abs(params$A-old_params$A))
    delta_B <- max(abs(params$B-old_params$B))
    delta_Pi <- max(abs(params$Pi-old_params$Pi))
    tmp_delta <-  c(delta_A,delta_B,delta_Pi)
    cat("Iter: ", n,"\n",
      "delta: ", tmp_delta,"\n")
    if ( all(tmp_delta < criterion) | (n == maxIter)) {
      print(params)
      cat("delta: ", tmp_delta,"\n",
          "Iter: ", n,"\n")
      return(params)
    }
  }
}

random_init <- function(Q,V){
  N <- length(Q) 
  M <- length(V)
  params <- list(
    A = matrix(nrow = N,ncol = N),
    B = matrix(nrow = N,ncol = M,dimnames = list(Q,V)),
    Pi = c()
    )

  for (i in 1:N) {
    temp <- runif(N,0,100)
    Sum <- sum(temp)
    for (j in 1:N) {
      params$A[i,j] = temp[j]/Sum
    }
  }

  for (i in 1:N) {
    temp <- runif(M,0,100)
    Sum <- sum(temp)
    for (j in 1:M) {
      params$B[i,j] = temp[j]/Sum
    }
  }

  temp <- runif(N,0,100)
  Sum <- sum(temp)
  params$Pi = temp/Sum
  return(params)
}
set.seed(1)
Q <- c(1,2,3) 
V <- c("R","W")
O <- c("R","W","R")
params <- random_init(Q,V)
params <- hmm_run(params = params,O,Q,V,maxIter=3)

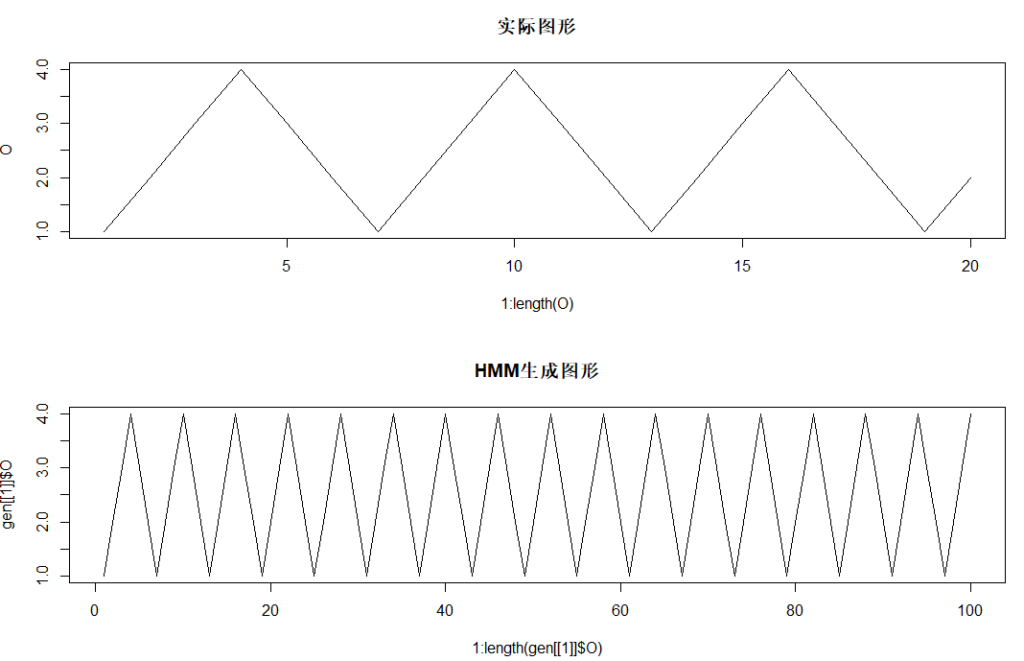
R示例：HMM生成三角波图形

hmm_sim_data <- function(params,n,len){
  gen_data <- function(len = len){
    temp_I <- sample(Q,1,replace = T,prob = params$Pi)
    I <- c(temp_I)
    temp_O <- sample(V,1,replace = T,prob = params$B[temp_I,])
    O <- c(temp_O)

    for (i in 2:len) {
      temp_I  <- sample(Q,1,replace = T,prob = params$A[temp_I,])
      I <- c(I,temp_I)
    }

    for (i in 2:len) {
      temp_O <- sample(V,1,replace = T,prob = params$B[I[i],])
      O <- c(O,temp_O)
    }
    return(list(I = I,O = O))
  }

  sim_data <- list()
  for (x in 1:n) {
    sim_data[[x]] <- gen_data(len = len)
  }
  return(sim_data)
}

set.seed(1)
Q <- 1:10
V <-  1:4
# 模拟三角波
O <- c(1,2,3,4,3,2,1,2,3,4,3,2,1,2,3,4,3,2,1,2)
par(mfrow=c(2,1))
plot(1:length(O),O,type = 'l',main = "实际图形")

params <- random_init(Q,V)
params <- hmm_run(params = params,O,Q,V,maxIter=100,criterion = 10e-6)

gen <- hmm_sim_data(params,n = 1,len = 100)
plot(1:length(gen[[1]]$O),gen[[1]]$O,type = "l",main = "HMM生成图形")

一、监督学习方法

二、无监督学习（Baum-Welch 算法）

相关文章

隐马尔可夫模型(HMM)（三）

隐马尔可夫模型(HMM)(一)

EM算法

留下评论取消回复