隐马尔可夫模型(HMM)（三）

HMM预测问题：
已知模型$\lambda=(A, B, \pi)$和观测序列$O＝(o_1，o_2,\cdots,o_T)$，求对给定观测序列条件概率$P(I|O)$最大的状态序列$I＝(i_1，i_2,\cdots,i_T)$,作为预测结果。

一、近似算法

在每个时刻 $t$ 选择在该时刻最可能出现的状态 $i_t^*$, 从而得到一个状态序列 $I^*＝(i_1^*，i_2^*,\cdots,i_T^*)$。

给定HMM模型 $\lambda$ 和观测序列 $O$, 在时刻 $t$ 处于状态 $q_i$ 的概率 $\gamma_t(i)$ 是

$$ \gamma_t(i) = \frac{\alpha_t(i)\beta_t(i) }{\sum_{j=1}^N{\alpha_t(j)\beta_t(j)}} $$

在每一时刻 $t$ 最有可能的状态 $i_t^*$ 是
$$
i_t^*=arg\max _{1\le i \le N} [\gamma_t(i)], i=1,2, \cdots, T $$

从而得到状态序列 $I^*＝(i_1^*，i_2^*,\cdots,i_T^*)$
近似算法计算简单，但不能保证预测的状态序列整体最优。

R示例：近似算法
已知模型的$\lambda=(A,B,\pi)$, 和观测序列$O$, 用近似法试求最优路径$I^*＝(i_1^*,i_2^*,i_3^*)$

# 模型参数
A <- matrix(c(0.5,0.3,0.2,0.2,0.5,0.3,0.3,0.2,0.5),nrow = 3) # 状态转移概率矩阵
B <- matrix(c(0.5,0.4,0.7,0.5,0.6,0.3),nrow = 3,dimnames = list(Q,V))  # 观测概率矩阵
Pi <- c(0.2,0.4,0.4)
# 观测序列
O <- c("R","W","R") 

V <- c("R","W") # 可能观测集合
Q <- c(1,2,3) # 可能状态集合
T_ <- length(O) # 观测数
N <- length(Q) # 状态数


# 近似算法
forward <- function(A,B,Pi,T_){
  alpha <- list()
  for (t in 1:T_) {
    if (t == 1) {
      alpha[[t]] <- Pi * B[,O[t]]
    } else {
      alpha[[t]] <- colSums(alpha[[t-1]] * A) * B[,O[t]]
    }
  }
  return(alpha)
}

backward <- function(A,B,N,T_){
  beta <- list()
  for (t in T_:1) {
    if (t == T_) {
      beta[[t]] <- rep(1,N)
    } else {
      beta[[t]] <- colSums(t(A) * B[,O[t+1]]*beta[[t+1]])
    }
  }
  return(beta)
}

gamma <- function(alpha,beta,i,t,N){
  numerator <- alpha[[t]][i]*beta[[t]][i]
  denominator <- 0
  for (j in 1:N) {
    denominator <- denominator+ alpha[[t]][j]*beta[[t]][j]
  }
  return(numerator/denominator)
}

approx_alg <- function(){
  alpha <- forward(A,B,Pi,T_)
  beta <- backward(A,B,N,T_)
  res <- list()
  for (t in 1:T_) {
    i_t <- c()
    for (i in 1:N) {
      i_t <- c(i_t,gamma(alpha,beta,i,t,N)  
    }
    res$p[[t]] <- i_t
    res$I[t] <- which.max(i_t)
  }
  return(res)
}
res1 <- approx_alg()
print(res1)

二、维特比算法

维特比算法（viterbi）应用动态规划高效地求解最优路径，即概率最大的状态序列。

引入变量 $\delta$, 表示在 $t$ 时刻状态为 $i$ 的所有单个路径 $(i_1，i_2,\cdots,i_T)$ 中概率最大值：
$$\delta_{t}(i)=\max_{i_1, i_2, \cdots, i_{t-1}} P(i_t=i, i_{t-1}, \cdots, i_1, o_t, \cdots, o_1 \mid \lambda), i=1,2, \cdots, N$$
递推得：
$$\begin{aligned}
\delta_{t+1}(i)=\max_{i_1, i_2, \cdots, i_t} P(i_{t+1}=i, i_t, \cdots, i_1, o_{t+1}, \cdots, o_1 \mid \lambda) \\ = \max_{1\le j\le N} [\delta_t(j)a_{ji}]b_i(o_{t+1}), i=1,2, \cdots, N; t=1,2, \cdots, T-1
\end{aligned}$$

变量 $\psi$ 表示时刻 $t$ 状态为 $i$ 得所有单个路径 $(i_1，i_2,\cdots,i_T)$ 中概率最大的路径的第 $t-1$个节点为:
$$
\psi_{t}(i)=arg\max_{1\le j\le N} [\delta_{t-1}(j)a_{ji}], i=1,2, \cdots, N
$$

计算过程：
输入: 模型 $\lambda=(A, B, \pi)$ 和观测 $O=(o_1,o_2,\cdots,o_T)$
输出: 最优路径 $I^*＝(i_1^*，i_2^*,\cdots,i_T^*)$
(1) 初始化。
$$\delta_1=\pi_ib_i(o_1), \psi_1(i)=0, i = 1,2,\cdots,N$$
(2) 递推。对 $t=2,3,\cdots,T; i=1,2, \cdots, N$

$$
\begin{aligned}
\delta_{t+1}(i) &=\max_{i_1, i_2, \cdots, i_t} P(i_{t+1}=i, i_t, \cdots, i_1, o_{t+1}, \cdots, o_1 \mid \lambda) \\
&= \max_{1\le j\le N} [\delta_t(j)a_{ji}]b_i(o_{t+1}), i=1,2, \cdots, N; t=1,2, \cdots, T-1
\end{aligned}
$$
(3) 终止。
$$P^*= \max_{1\le i\le N} \delta_T(i)$$
(4) 最优路径回溯。对 $t=T-1,T-2,\cdots,1$
$$i_T^*=\psi_{t+1}(i_{t+1}^*)$$

R示例：维特比算法
同上条件，用维特比算法试求最优路径$I^*＝(i_1^*,i_2^*,i_3^*)$

# 维特比算法
viterbi <- function(){
  delta <- list()
  psi <- list()
  for (t in 1:T_) {
    delta[[t]] <- rep(NA,N)
    psi[[t]] <- rep(NA,N)
    if (t ==1) {
      delta[[t]] <- as.vector(Pi*B[,O[1]])
      psi[[t]] <- rep(0,N)
      next
    }
    for (i in 1:N) {
      delta_A <- delta[[t-1]]*A[,i]
      delta[[t]][i] <- max(delta_A*B[i,O[t]])
      psi[[t]][i] <- which.max(delta_A)
    }
  }
  I <- rep(NA,T_)
  P <- max(delta[[T_]])
  I[T_] <- which.max(delta[[T_]])
  for (t in (T_-1):1) {
    I[t] <- psi[[t+1]][I[t+1]]
  }
  return(list(delta = delta,psi = psi,maxP = P, I=I))
}
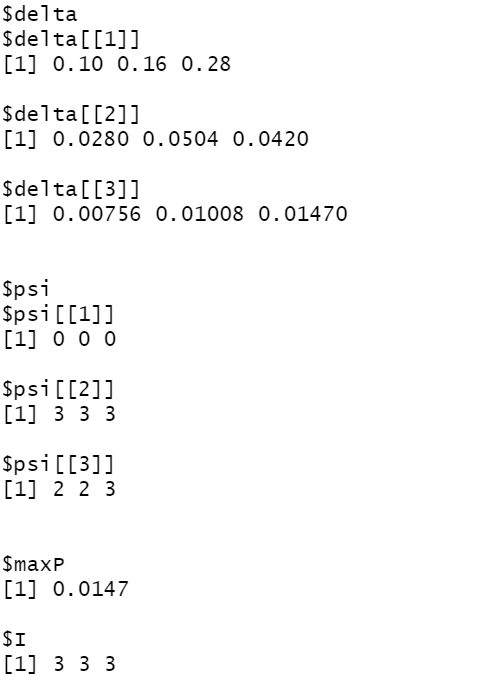
res2 <- viterbi()
print(res2)