隐马尔可夫模型(HMM)(一)

一、隐马尔可夫模型(HMM)

隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态的序列，再由各个状态随机生成一个观测而产生观测的序列的过程。
隐马尔可夫模型由初始状态概率向$\pi$、状态转移概率矩阵$A$和观测概率矩阵$B$决定。因此，隐马尔可夫模型可以写成$\lambda=(A, B, \pi)$。
隐马尔可夫模型是一个生成模型，表示状态序列和观测序列的联合分布，但是状态序列是隐藏的，不可观测的。

定义：
设 $Q$ 是所有可能状态的集合，$V$是所有可能的观测的集合：
$$Q={q_1,q_2,\cdots,q_N}, V={v_1,v_2,\cdots,v_M}$$
其中，$N$ 是可能状态数，$M$ 是可能观测数。
$I$ 是长度为 $T$ 的状态序列， $O$ 是对应的观测序列：
$$I={i_1,i_2,\cdots,i_T}, O={o_1,o_2,\cdots,o_T}$$
$A$ 是状态转移概率矩阵：$A=[a_{ij}]_{N*N}$ 其中, $a{ij} = P(i_{t+1}=q_j | i_t=q_i), i=1,2,\cdots,N;j=1,2,\cdots,N$
是在时刻 $t$ 处于状态 $q_i$ 的条件下在时刻 $t+1$ 转移到状态 $q_j$ 的概率。

$B$ 是观测概率矩阵：$B=[b_{j}(K)]_{N*M}$ 其中, $b{j}(K) = P(o_{t}=v_k | i_t=q_j), k=1,2,\cdots,M; j=1,2,\cdots,N$
是在时刻 $t$ 处于状态 $q_j$ 的条件下生成观测概率 $v_k$ 的概率。

$\pi$ 是初始状态概率向量：$\pi=(\pi_i)$
其中, $\pi_i = P(i_1=q_i), i=1,2,\cdots,N$
是时刻 $t=1$ 处于状态 $q_i$ 的条概率。

隐马尔可夫模型两个基本假设：

齐次马尔科夫假设，即假设隐藏的马尔可夫链在任意时刻的状态只依赖于其前一时刻的状态，与其他时刻的状态及观测无关，也与时刻无关。
观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测及状态无关。

隐马尔可夫模型的三个基本问题：

概率计算问题。给定模型$\lambda=(A, B, \pi)$和观测序列$O＝(o_1，o_2,\cdots,o_T)$，计算在模型$\lambda$下观测序列$O$出现的概率$P(O|\lambda)$。前向-后向算法是通过递推地计算前向-后向概率可以高效地进行隐马尔可夫模型的概率计算。
学习问题。已知观测序列$O＝(o_1，o_2,\cdots,o_T)$，估计模型$\lambda=(A, B, \pi)$参数，使得在该模型下观测序列概率$P(O|\lambda)$最大。即用极大似然估计的方法估计参数。Baum-Welch算法，也就是EM算法可以高效地对隐马尔可夫模型进行训练。它是一种非监督学习算法。
预测问题。已知模型$\lambda=(A, B, \pi)$和观测序列$O＝(o_1，o_2,\cdots,o_T)$，求对给定观测序列条件概率$P(I|O)$最大的状态序列$I＝(i_1，i_2,\cdots,i_T)$。维特比算法应用动态规划高效地求解最优路径，即概率最大的状态序列。

二、概率计算算法

HMM概率计算问题：
给定模型$\lambda=(A, B, \pi)$和观测序列$O＝(o_1，o_2,\cdots,o_T)$，计算在模型$\lambda$下观测序列$O$出现的概率$P(O|\lambda)$。前向-后向算法是通过递推地计算前向-后向概率可以高效地进行隐马尔可夫模型的概率计算。
计算观测序列概率$P(O|\lambda)$的前向(forward)与后向(backward)算法。

2.1 前向概率

给定隐马尔可夫模型$\lambda$，定义时刻$t$部分的观测序列为$o_1,o_2,…,o_t$且状态为$q_i$的概率为前向概率，记作：
$$\alpha_t(i)=P(o_1,o_2,\cdots,o_t,i_t=q_i |\lambda)$$
可递推求得前向概率$\alpha_t(i)$及观测序列概率$P(O|\lambda)$。

观测序列概率的前向算法：
输入：隐马尔可夫模型$\lambda$，观测序列 $O$。
输出：观测序列概率$P(O|\lambda)$

step 1：
初值：$\alpha_1(i)=\pi_ib_i(o_1),i=1,2,\cdots,N$
step 2:
递推：对$t=1,2,\cdots,T-1$,
$$\alpha_{t+1}=\bigg[\sum_{j=1}^N\alpha_t(j)a_{ji}\bigg]b_i(o_{t+1}),i=1,2,\cdots,N$$
step 3:
终止：$P(O|\lambda)=\sum_{i=1}^N\alpha_T(i)$

例1：给定盒子和球组成的隐马尔可夫模型$\lambda=(A,B,\pi)$，状态集合$Q=\{1,2,3\}$，观测集合$V=\{红, 白\}$，
$$A=\left[\begin{array}{ccc}0.5&0.2&0.3\\0.3&0.5&0.2\\0.2&0.3&0.5\end{array}\right], \quad B=\left[\begin{array}{cc}0.5&0.5\\0.4&0.6\\0.7&0.3\end{array}\right], \quad \pi=(0.2,0.4,0.4)^T$$
设$T=3, O=(红, 白, 红)$，试用前向算法计算$P(O|\lambda)$。

Q <- c(1,2,3) # 可能状态集合
N <- length(Q) # 状态数
V <- c("R","W") # 可能观测集合
A <- matrix(c(0.5,0.3,0.2,0.2,0.5,0.3,0.3,0.2,0.5),nrow = 3) # 状态转移概率
B <- matrix(c(0.5,0.4,0.7,0.5,0.6,0.3), 
            nrow = 3,dimnames = list(Q,V))  # 观测概率
Pi <- c(0.2,0.4,0.4) # 初始状态

O <- c("R","W","R") # 对应的观测序列
T_ <- length(O) # 观测数

# forward
alpha <- list()
for (t in 1:T_) {  # 时刻数=观测数
  if (t == 1) {
    alpha[[t]] <- Pi*B[,O[t]]
  } else {
    alpha[[t]] <- colSums(alpha[[t-1]] * A) * B[,O[t]]
  }
}
P <- sum(alpha[[T_]])
print(alpha)
print(P)

2.2 后向概率

给定隐马尔可夫模型$\lambda$，定义时刻 $t$ 部分的观测序列为$o_1,o_2,…,o_t$且状态为 $q_i$ 的概率为前向概率，记作：
$$\beta_t(i)=P(o_1,o_2,\cdots,o_t|i_t=q_i, \lambda)$$
可递推求得前向概率 $\alpha_t(i)$ 及观测序列概率 $P(O|\lambda)$。

观测序列概率的后向算法：
输入：隐马尔可夫模型$\lambda$，观测序列 $O$。
输出：观测序列概率$P(O|\lambda)$

step 1：
初值：$\beta_T(i)=1,i=1,2,\cdots,N$
step 2:
递推：对$t=T-1,T-2,\cdots,1$
$$\beta_{t}(i)=\sum_{j=1}^Na_{ij}b_j(o_{t+1})\beta_{t+1}(j),i=1,2,\cdots,N$$
step 3:
终止：$P(O|\lambda)=\sum_{i=1}^N\pi_ib_i(o_1)\beta_1(i)$

例2:
同例1，试用后向算法计算$P(O|\lambda)$。

beta <- list()
for (t in T_:1) {  # 时刻数=观测数
  if (t == T_) {
    beta[[t]] <- rep(1,N)
  } else {
    beta[[t]] <- colSums(t(A) * B[,O[t+1]] * beta[[t+1]])
  }
}

P2 <- sum(Pi*B[,O[1]]*beta[[1]])
print(beta)
print(P2)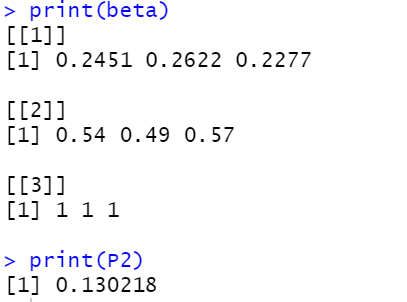

例3:
同例1，设$T=8,O=(红,白,红,红,白,红,白,白)$，试计算$P(i_4=q_3|O,\lambda)$。
$$\displaystyle P(i_4=q_3|O,\lambda)=\frac{P(i_4=q_3,O|\lambda)}{P(O|\lambda)}=\frac{\alpha_4(3)\beta_4(3)}{P(O|\lambda)}$$

O <- c("R","W","R","R","W","R","W","W") 
M <- length(O) # 观测数

# forward
alpha <- list()
for (t in 1:T_) {  # 时刻数=观测数
  if (t == 1) {
    alpha[[t]] <- Pi * B[,O[t]]
  } else {
    alpha[[t]] <- colSums(alpha[[t-1]] * A) * B[,O[t]]
  }
}
P <- sum(alpha[[T_]])
# backward
beta <- list()
for (t in T_:1) {  # 时刻数=观测数
  if (t == T_) {
    beta[[t]] <- rep(1,N)
  } else {
    beta[[t]] <- colSums(t(A) * B[,O[t+1]]*beta[[t+1]])
  }
}
P2 <- sum(Pi*B[,O[1]]*beta[[1]])
res <- (alpha[[4]][3]*beta[[4]][3])/P)
print(res)
# 0.4340691

一、隐马尔可夫模型(HMM)

二、概率计算算法

2.1 前向概率

2.2 后向概率

相关文章

隐马尔可夫模型(HMM)（三）

隐马尔可夫模型(HMM)（二）

EM算法

留下评论取消回复