1. 两个随机变量
到目前为止,我们已经考虑了单个随机变量。然而,在许多情况下,在随机实验中,我们可能有不止一个感兴趣的量。例如,在一个我们掷硬币十次的实验中,我们可能既关心$X(\omega) =$出现的正面数量,也关心$Y (\omega) =$连续最长出现正面的长度。在本节中,我们考虑两个随机变量的设置。
1.1 联合分布和边缘分布
假设我们有两个随机变量,一个方法是分别考虑它们。如果我们这样做,我们只需要$F_X (x)$和$F_Y (y)$。但是如果我们想知道在随机实验的结果中,$X$和$Y$同时假设的值,我们需要一个更复杂的结构,称为$X$和$Y$的联合累积分布函数,定义如下:
$$
F_{XY}(x,y)=P(X \leq x,Y \leq y)
$$
可以证明,通过了解联合累积分布函数,可以计算出任何涉及到$X$和$Y$的事件的概率。
联合CDF: $F_{XY }(x,y)$和每个变量的联合分布函数$F_X(x)$和$F_Y (y)$分别由下式关联:
$$
F_{X}(x)=\lim {y \rightarrow \infty} F_{X Y}(x, y) d y
$$
$$
F_{Y}(y)=\lim {y \rightarrow \infty} F_{X Y}(x, y) dx
$$
这里我们称$F_X(x)$和$F_Y (y)$为 $F_{XY }(x,y)$的边缘累积概率分布函数。
性质:
- $0 \leq F_{XY }(x,y) \leq 1$
- $\lim {x, y \rightarrow \infty} F_{X Y}(x, y)=1$
- $\lim {x, y \rightarrow -\infty} F_{X Y}(x, y)=0$
- $F_{X}(x)=\lim {y \rightarrow \infty} F_{X Y}(x, y)$
1.2 联合概率和边缘概率质量函数
如果$X$和$Y$是离散随机变量,那么联合概率质量函数 $p_{X Y} : \mathbb{R} \times \mathbb{R} \rightarrow [0,1]$由下式定义:
$$
p_{X Y}(x,y)=P(X=x,Y=y)
$$
这里, 对于任意$x$,$y$,$0 \leq P_{XY} (x,y) \leq 1$, 并且 $\sum_{x \in V a l(X)} \sum_{y \in V a l(Y)} P_{X Y}(x, y)=1$
两个变量上的联合PMF分别与每个变量的概率质量函数有什么关系?事实上:
$$
p_{X}(x)=\sum_{y} p_{X Y}(x, y)
$$
对于$p_Y (y)$类似。在这种情况下,我们称$p_X(x)$为$X$的边际概率质量函数。在统计学中,将一个变量相加形成另一个变量的边缘分布的过程通常称为“边缘化”。
1.3 联合概率和边缘概率密度函数
假设$X$和$Y$是两个连续的随机变量,具有联合分布函数$F_{XY}$。在$F_{XY}(x,y)$在$x$和$y$中处处可微的情况下,我们可以定义联合概率密度函数:
$$
f_{X Y}(x, y)=\frac{\partial^{2} F_{X Y}(x, y)}{\partial x \partial y}
$$
如同在一维情况下,$f_{XY}(x,y)\not= P(X = x,Y = y)$,而是:
$$
\iint_{x \in A} f_{X Y}(x, y) d x d y=P((X, Y) \in A)
$$
请注意,概率密度函数$f_{XY}(x,y)$的值总是非负的,但它们可能大于1。尽管如此,可以肯定的是 $\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f_{X Y}(x, y)=1$
与离散情况相似,我们定义:
$$
f_{X}(x)=\int_{-\infty}^{\infty} f_{X Y}(x, y) d y
$$
作为$X$的边际概率密度函数(或边际密度),对于$f_Y (y)$也类似。
1.4 条件概率分布
条件分布试图回答这样一个问题,当我们知道$X$必须取某个值$x$时,$Y$上的概率分布是什么?在离散情况下,给定$Y$的条件概率质量函数是简单的:
$$
p_{Y | X}(y | x)=\frac{p_{X Y}(x, y)}{p_{X}(x)}
$$
假设分母不等于0。
在连续的情况下,在技术上要复杂一点,因为连续随机变量的概率等于零。忽略这一技术点,我们通过类比离散情况,简单地定义给定$X = x$的条件概率密度为:
$$
f_{Y | X}(y | x)=\frac{f_{X Y}(x, y)}{f_{X}(x)}
$$
假设分母不等于0。
1.5 贝叶斯定理
当试图推导一个变量给定另一个变量的条件概率表达式时,经常出现的一个有用公式是贝叶斯定理。
对于离散随机变量$X$和$Y$:
$$
P_{Y | X}(y | x)=\frac{{P_{XY}}(x, y)}{P_{X}(x)}=\frac{P_{X | Y}(x | y) P_{Y}(y)}{\sum_{y^{\prime} \in V a l(Y)} P_{X | Y}\left(x | y^{\prime}\right) P_{Y}\left(y^{\prime}\right)}
$$
对于连续随机变量$X$和$Y$:
$$
f_{Y | X}(y | x)=\frac{f_{X Y}(x, y)}{f_{X}(x)}=\frac{f_{X | Y}(x | y) f_{Y}(y)}{\int_{-\infty}^{\infty} f_{X | Y}\left(x | y^{\prime}\right) f_{Y}\left(y^{\prime}\right) d y^{\prime}}
$$
1.6 独立性
如果对于$X$和$Y$的所有值,$F_{XY}(x,y) = F_X(x)F_Y(y)$,则两个随机变量$X$和$Y$是独立的。等价地,
- 对于离散随机变量, 对于任意$x \in Val(X)$, $y \in Val(Y)$ ,$p_{XY}(x,y) = p_X (x)p_Y (y)$。
- 对于离散随机变量, $p_Y |X (y|x) = p_Y (y)$当对于任意$y \in Val(Y)$且$p_X (x) \not= 0$。
- 对于连续随机变量, $f_{XY}(x,y) = f_X (x)f_Y(y)$ 对于任意 $x,y \in \mathbb{R}$。
- 对于连续随机变量, $f_{Y |X} (y|x) = f_Y (y)$ ,当$f_X (x)\not = 0$对于任意$y \in \mathbb{R}$。
非正式地说,如果“知道”一个变量的值永远不会对另一个变量的条件概率分布有任何影响,那么两个随机变量$X$和$Y$是独立的,也就是说,你只要知道$f(x)$和$f(y)$就知道关于这对变量$(X,Y)$的所有信息。以下引理将这一观察形式化:
引理3.1
如果$X$和$Y$是独立的,那么对于任何$A,B⊆ \mathbb{R}$,我们有:
$$
P(X \in A, Y \in B)=P(X \in A) P(Y \in B)
$$
利用上述引理,我们可以证明如果$X$与$Y$无关,那么$X$的任何函数都与$Y$的任何函数无关。
1.7 期望和协方差
假设我们有两个离散的随机变量$X$,$Y$并且$g : \mathbf{R}^{2} \longrightarrow \mathbf{R}$是这两个随机变量的函数。那么$g$的期望值以如下方式定义:
$$
E[g(X, Y)] \triangleq \sum_{x \in V a l(X)} \sum_{y \in V a l(Y)} g(x, y) p_{X Y}(x, y)
$$
对于连续随机变量$X$,$Y$,类似的表达式是:
$$
E[g(X, Y)]=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} g(x, y) f_{X Y}(x, y) d x d y
$$
我们可以用期望的概念来研究两个随机变量之间的关系。特别地,两个随机变量的协方差定义为:
$$
{Cov}[X, Y] \triangleq E[(X-E[X])(Y-E[Y])]
$$
使用类似于方差的推导,我们可以将它重写为:
$$
\begin{aligned} {Cov}[X, Y] &=E[(X-E[X])(Y-E[Y])] \\ &=E[X Y-X E[Y]-Y E[X]+E[X] E[Y]] \\ &=E[X Y]-E[X] E[Y]-E[Y] E[X]+E[X] E[Y]] \\ &=E[X Y]-E[X] E[Y] \end{aligned}
$$
在这里,说明两种协方差形式相等的关键步骤是第三个等号,在这里我们使用了这样一个事实,即$E[X]$和$E[Y]$实际上是常数,可以被提出来。当$cov[X,Y] = 0$时,我们说$X$和$Y$不相关。
性质:
- (期望线性) $E[f(X,Y ) + g(X,Y)] = E[f(X,Y )] + E[g(X,Y)]$
- $V ar[X + Y ] = V ar[X] + V ar[Y ] + 2Cov[X,Y]$
- 如果$X$和$Y$相互独立, 那么 $Cov[X,Y ] = 0$
- 如果$X$和$Y$相互独立, 那么 $E[f(X)g(Y )] = E[f(X)]E[g(Y)]$.
2. 多个随机变量
上一节介绍的概念和想法可以推广到两个以上的随机变量。特别是,假设我们有$n$个连续随机变量,$X _1 (\omega),X_2 (\omega),\cdots X_n (\omega)$。在本节中,为了表示简单,我们只关注连续的情况,对离散随机变量的推广工作类似。
2.1 基本性质
我们可以定义$X_1,X_2,\cdots,X_n$的联合累积分布函数、联合概率密度函数,以及给定$X_2,\cdots,X_n$时$X_1$的边缘概率密度函数为:
$$
F_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right)=P\left(X_{1} \leq x_{1}, X_{2} \leq x_{2}, \ldots, X_{n} \leq x_{n}\right)
$$
$$
f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right)=\frac{\partial^{n} F_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right)}{\partial x_{1} \ldots \partial x_{n}}
$$
$$
f_{X_{1}}\left(X_{1}\right)=\int_{-\infty}^{\infty} \cdots \int_{-\infty}^{\infty} f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right) d x_{2} \ldots d x_{n}
$$
$$
f_{X_{1} | X_{2}, \ldots, X_{n}}\left(x_{1} | x_{2}, \dots x_{n}\right)=\frac{f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \dots x_{n}\right)}{f_{X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right)}
$$
为了计算事件$A \subseteq \mathbb{R}^{n}$的概率,我们有:
$$
P\left(\left(x_{1}, x_{2}, \ldots x_{n}\right) \in A\right)=\int_{\left(x_{1}, x_{2}, \ldots x_{n}\right) \in A} f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right) d x_{1} d x_{2} \ldots d x_{n}
$$
链式法则:
从多个随机变量的条件概率的定义中,可以看出:
$$
\begin{aligned} f\left(x_{1}, x_{2}, \ldots, x_{n}\right) &=f\left(x_{n} | x_{1}, x_{2} \ldots, x_{n-1}\right) f\left(x_{1}, x_{2} \ldots, x_{n-1}\right) \\ &=f\left(x_{n} | x_{1}, x_{2} \ldots, x_{n-1}\right) f\left(x_{n-1} | x_{1}, x_{2} \ldots, x_{n-2}\right) f\left(x_{1}, x_{2} \ldots, x_{n-2}\right) \\&=\cdots=f\left(x_{1}\right) \prod_{i=2}^{n} f\left(x_{i} | x_{1}, \ldots, x_{i-1}\right) \end{aligned}
$$
独立性:对于多个事件,$A_1,\cdots ,A_k$,我们说$A_1,\cdots ,A_k$ 是相互独立的,当对于任何子集$S \subseteq {1,2,\cdots,k}$,我们有:
$$
P\left(\cap_{i \in S} A_{i}\right)=\prod_{i \in S} P\left(A_{i}\right)
$$
同样,我们说随机变量$X_1,X_2,\cdots,X_n$是独立的,如果:
$$
f(x_1,\cdots,x_n)=f(x_1)f(x_2)\cdots f(x_n)
$$
这里,相互独立性的定义只是两个随机变量独立性到多个随机变量的自然推广。
独立随机变量经常出现在机器学习算法中,其中我们假设属于训练集的训练样本代表来自某个未知概率分布的独立样本。为了明确独立性的重要性,考虑一个“坏的”训练集,我们首先从某个未知分布中抽取一个训练样本$(x^{ (1)},y^{(1)})$,然后将完全相同的训练样本的$m-1$个副本添加到训练集中。在这种情况下,我们有:
$$
P\left(\left(x^{(1)}, y^{(1)}\right), \ldots .\left(x^{(m)}, y^{(m)}\right)\right) \neq \prod_{i=1}^{m} P\left(x^{(i)}, y^{(i)}\right)
$$
尽管训练集的大小为$m$,但这些例子并不独立!虽然这里描述的过程显然不是为机器学习算法建立训练集的明智方法,但是事实证明,在实践中,样本的不独立性确实经常出现,并且它具有减小训练集的“有效大小”的效果。
2.2 随机向量
假设我们有n个随机变量。当把所有这些随机变量放在一起工作时,我们经常会发现把它们放在一个向量中是很方便的…我们称结果向量为随机向量(更正式地说,随机向量是从$\Omega$到$\mathbb{R}^n$的映射)。应该清楚的是,随机向量只是处理$n$个随机变量的一种替代符号,因此联合概率密度函数和综合密度函数的概念也将适用于随机向量。
期望:
考虑$g : \mathbb{R}^n \rightarrow \mathbb{R}$中的任意函数。这个函数的期望值 被定义为
$$
E[g(X)]=\int_{\mathbb{R}^{n}} g\left(x_{1}, x_{2}, \ldots, x_{n}\right) f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right) d x_{1} d x_{2} \ldots d x_{n}E[g(X)] \\ =\int_{\mathbb{R}^{n}} g\left(x_{1}, x_{2}, \ldots, x_{n}\right) f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right) d x_{1} d x_{2} \ldots d x_{n}
$$
其中,$\int_{\mathbb{R}^{n}}$是从$-\infty$到$\infty$的$n$个连续积分。如果$g$是从$\mathbb{R}^n$到$\mathbb{R}^m$的函数,那么$g$的期望值是输出向量的元素期望值,即,如果$g$是:
$$g(x)=\begin{bmatrix}
g_1(x)\\
g_2(x)\\
\vdots \\
g_mm(x)
\end{bmatrix}$$
那么,
$$
E(g(x))=\begin{bmatrix}
E(g_1(x))\\
E(g_2(x))\\
\vdots \\
E(g_mm(x))
\end{bmatrix}
$$
协方差矩阵:对于给定的随机向量$X:\Omega\rightarrow \mathbb{R}^n$,其协方差矩阵$\Sigma$是$n \times n$平方矩阵,其输入由$\Sigma_{i j}={Cov}\left[X_{i}, X_{j}\right]$给出。从协方差的定义来看,我们有:
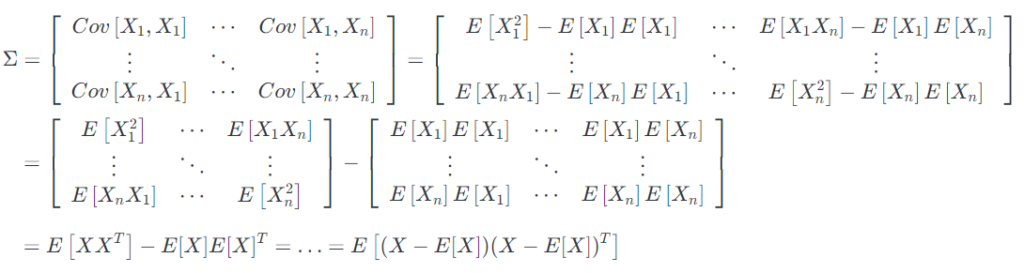
其中矩阵期望以明显的方式定义。
协方差矩阵有许多有用的属性:
- $\Sigma \succeq 0$;也就是说,$\Sigma$是正半定的。
- $\Sigma=\Sigma^T$;也就是说,$\Sigma$是对称的。
2.3 多元高斯分布
随机向量上概率分布的一个特别重要的例子叫做多元高斯或多元正态分布。随机向量$X\in \mathbb{R}^n$被认为具有多元正态(或高斯)分布,当其具有均值$\mu \in \mathbb{R}^n$和协方差矩阵$\Sigma \in \mathbb{S}{++}^{n}$(其中$ \mathbb{S}{++}^{n}$指对称正定$n \times n$矩阵的空间)
$f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots, x_{n} ; \mu, \Sigma\right)=\frac{1}{(2 \pi)^{n / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)\right)$
我们把它写成$X \sim \mathcal{N}(\mu, \Sigma)$。请注意,在$n = 1$的情况下,它降维成普通正态分布,其中均值参数为$\mu_1$,方差为$\Sigma_{11}$。
一般来说,高斯随机变量在机器学习和统计中非常有用,主要有两个原因:
首先,在统计算法中对“噪声”建模时,它们非常常见。通常,噪声可以被认为是影响测量过程的大量小的独立随机扰动的累积;根据中心极限定理,独立随机变量的总和将趋向于“看起来像高斯”。
其次,高斯随机变量便于许多分析操作,因为实际中出现的许多涉及高斯分布的积分都有简单的封闭形式解。。
