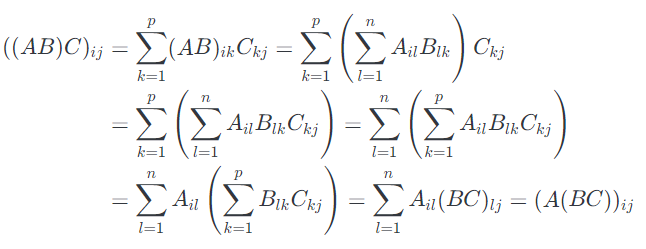1. 基础概念和符号
线性代数提供了一种紧凑地表示和操作线性方程组的方法。 例如,以下方程组:
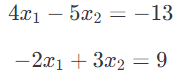
这是两个方程和两个变量,正如你从高中代数中所知,你可以找到 $x_1$ 和 $x_2$ 的唯一解(除非方程以某种方式退化,例如,如果第二个方程只是第一个的倍数,但在上面的情况下,实际上只有一个唯一解)。 在矩阵表示法中,我们可以更紧凑地表达:
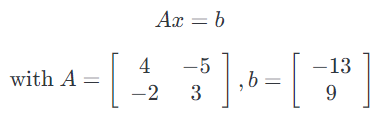
我们可以看到,这种形式的线性方程有许多优点(比如明显地节省空间)。
我们使用以下符号:
- $A \in \mathbb{R}^{m \times n}$,表示 $A$ 为由实数组成具有$m$行和$n$列的矩阵。
- $x \in \mathbb{R}^{ n}$,表示具有$n$个元素的向量。 通常,向量$x$将表示列向量: 即,具有$n$行和$1$列的矩阵。 如果我们想要明确地表示行向量: 具有 $1$ 行和$n$列的矩阵 – 我们通常写$x^T$(这里$x^T$$x$的转置)。
- $x_i$表示向量$x$的第$i$个元素
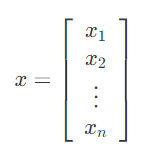
- 我们使用符号 $a_{ij}$(或$A_{ij}$,$A_{i,j}$等)来表示第 $i$ 行和第$j$列中的 $A$ 的元素:
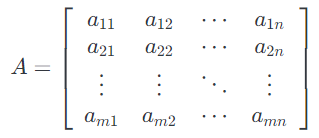
- 我们用$a^j$或者$A_{:,j}$表示矩阵$A$的第$j$列:
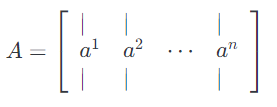
- 我们用$a^T_i$或者$A_{i,:}$表示矩阵$A$的第$i$行:
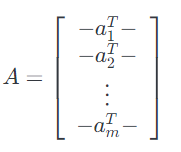
在许多情况下,将矩阵视为列向量或行向量的集合非常重要且方便。 通常,在向量而不是标量上操作在数学上(和概念上)更清晰。只要明确定义了符号,用于矩阵的列或行的表示方式并没有通用约定。
2. 矩阵乘法
两个矩阵相乘,其中 $A \in \mathbb{R}^{m \times n}$ and $B \in \mathbb{R}^{n \times p}$ ,则:
$$
C = AB \in \mathbb{R}^{m \times p}
$$
其中:
$$
C_{i j}=\sum_{k=1}^{n} A_{i k} B_{k j}
$$
请注意,为了使矩阵乘积存在,$A$中的列数必须等于$B$中的行数。有很多方法可以查看矩阵乘法,我们将从检查一些特殊情况开始。
2.1 向量-向量乘法
给定两个向量$x, y \in \mathbb{R}^{n}$,$x^T y$通常称为向量内积或者点积,结果是个实数。
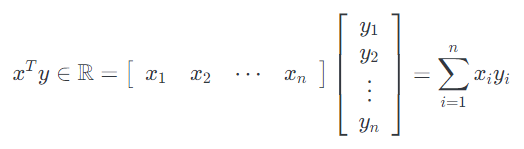
注意:$x^T y = y^Tx$ 始终成立。
给定向量 $x \in \mathbb{R}^{m}$, $y \in \mathbb{R}^{n}$ (他们的维度是否相同都没关系),$xy^T \in \mathbb{R}^{m \times n}$叫做**向量外积 ** , 当 $(xy^T)_{ij} = x_iy_j$ 的时候,它是一个矩阵。
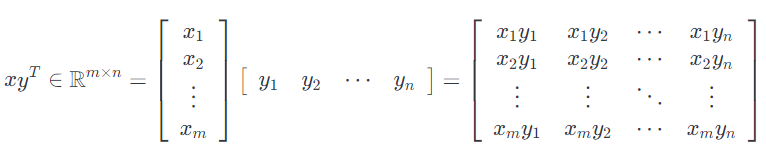
举一个外积如何使用的一个例子:让$1\in R^{n}$表示一个$n$维向量,其元素都等于1,此外,考虑矩阵$A \in R^{m \times n}$,其列全部等于某个向量 $x \in R^{m}$。 我们可以使用外积紧凑地表示矩阵 $A$:

2.2 矩阵-向量乘法
给定矩阵 $A \in \mathbb{R}^{m \times n}$,向量 $x \in \mathbb{R}^{n}$ , 它们的积是一个向量 $y = Ax \in R^{m}$。 有几种方法可以查看矩阵向量乘法,我们将依次查看它们中的每一种。
如果我们按行写$A$,那么我们可以表示$Ax$为:
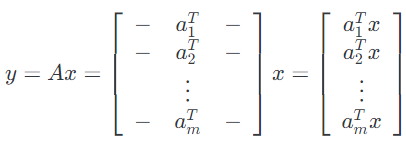
换句话说,第$i$个$y$是$A$的第$i$行和$x$的内积,即:$y_i = y_{i}=a_{i}^{T} x$。
同样的, 可以把 $A$ 写成列的方式,则公式如下:
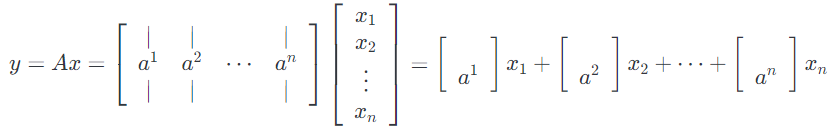
换句话说,$y$是$A$的列的线性组合,其中线性组合的系数由$x$的元素给出。
到目前为止,我们一直在右侧乘以列向量,但也可以在左侧乘以行向量。 这是写的,$y^T = x^TA$ 表示$A \in \mathbb{R}^{m \times n}$,$x \in \mathbb{R}^{m}$,$y \in \mathbb{R}^{n}$。 和以前一样,我们可以用两种可行的方式表达$y^T$,这取决于我们是否根据行或列表达$A$.
第一种情况,我们把$A$用列表示:
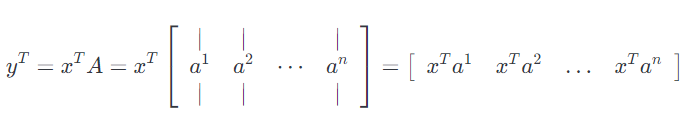
这表明$y^T$的第$i$个元素等于$x$和$A$的第$i$列的内积。
最后,根据行表示$A$,我们得到了向量-矩阵乘积的最终表示:
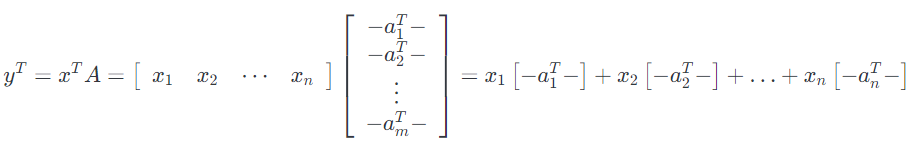
2.3 矩阵-矩阵乘法
有了这些知识,我们现在可以看看四种不同的(形式不同,但结果是相同的)矩阵-矩阵乘法:也就是本节开头所定义的$C=AB$的乘法。
首先,我们可以将矩阵 – 矩阵乘法视为一组向量-向量乘积。 从定义中可以得出:最明显的观点是$C $的$( i,j )$元素等于$A$的第$i$行和$B$的的$j$列的内积。如下面的公式所示:
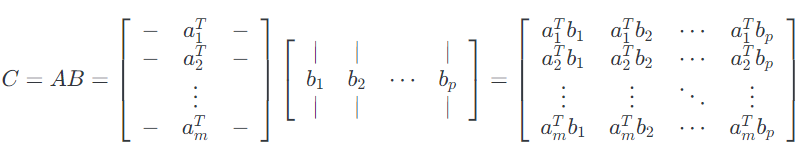
这里的$ A \in \mathbb{R}^{m\times n}$ ,$B \in \mathbb{R}^{n \times p}$, $a_i \in \mathbb{R}^n$ ,$b^j \in \mathbb{R}^{n \times p}$, 这里的$ A \in \mathbb{R}^ {m \times n},$ $B \in \mathbb{R}^ {n \times p} $, $a_i \in \mathbb{R} ^ n $,$ b ^ j \in \mathbb{R} ^ {n \times p} $,所以它们可以计算内积。 我们用通常用行表示$ A $而用列表示$B$。
或者,我们可以用列表示$ A$,用行表示$B $,这时$AB$是求外积的和。公式如下:
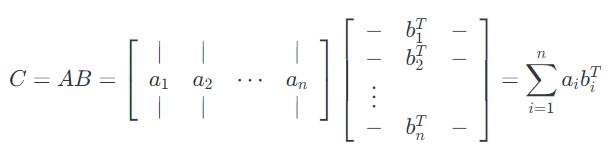
换句话说,$AB$等于所有的$A$的第$i$列和$B$第$i$行的外积的和。因此,在这种情况下, $a_i \in \mathbb{R}^ m $和$b_i \in \mathbb{R}^p$, 外积$a^ib_i^T$的维度是$m×p$,与$C$的维度一致。
其次,我们还可以将矩阵 – 矩阵乘法视为一组矩阵向量积。如果我们把$B$用列表示,我们可以将$C$的列视为$A$和$B$的列的矩阵向量积。公式如下:
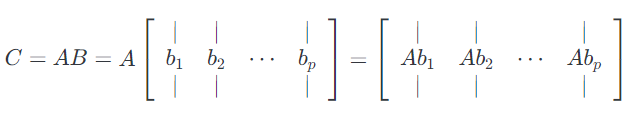
这里$C$的第$i$列由矩阵向量乘积给出,右边的向量为$c_i = Ab_i$。 这些矩阵向量乘积可以使用前一小节中给出的两个观点来解释。
最后,我们有类似的观点,我们用行表示$A$,$C$的行作为$A$和$C$行之间的矩阵向量积。公式如下:
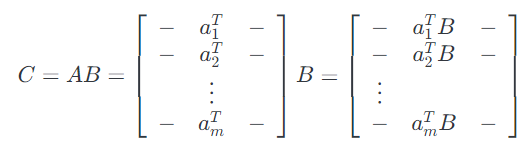
这里第$i$行的$C$由左边的向量的矩阵向量乘积给出:$c_i^T = a_i^T B$
将矩阵乘法剖析到如此大的程度似乎有点过分,特别是当所有这些观点都紧跟在我们在本节开头给出的初始定义(在一行数学中)之后。
这些不同方法的直接优势在于它们允许您在向量的级别/单位而不是标量上进行操作。 为了完全理解线性代数而不会迷失在复杂的索引操作中,关键是要用尽可能多的概念进行操作。
实际上所有的线性代数都处理某种矩阵乘法,花一些时间对这里提出的观点进行直观的理解是非常必要的。
除此之外,了解一些更高级别的矩阵乘法的基本属性是很有必要的:
- 矩阵乘法结合律: $(AB)C = A(BC)$
- 矩阵乘法分配律: $A(B + C) = AB + AC$
- 矩阵乘法通常不是可交换的; 也就是说,通常$AB \ne BA$。 (例如,假设$ A \in \mathbb{R}^ {m \times n},$ $B \in \mathbb{R}^ {n \times p} $,如果$m$和$q$不相等,矩阵乘积$BA$甚至不存在!)
- 矩阵乘法的相关性,假设$A \in \mathbb{R}^ {m \times n},$ $B \in \mathbb{R}^ {n \times p} $,$C \in \mathbb{R}^ {p \times q}$。 注意$AB \in \mathbb{R}^ {m \times p}$,所以$(AB)C \in \mathbb{R}^ {m \times q}$。 类似地,$BC \in \mathbb{R}^ {n \times q}$,所以$A(BC) \in \mathbb{R}^ {m \times q}$。 因此,所得矩阵的维度一致。 为了表明矩阵乘法是相关的,足以检查$(AB)C $的第$(i,j)$个元素是否等于$A(BC)$的第$(i,j)$个元素。 我们可以使用矩阵乘法的定义直接验证这一点: