正所谓物以类聚,人以群分。人们在获取数据时需要整理,将相似的数据归档到一起,自动发现大量样本之间的相似性,这种根据相似性归档的任务称为聚类。
一、概述
1.聚类。
聚类(cluster analysis )指的是将给定对象的集合划分为不同子集的过程,目标是使得每个子集内部的元素尽量相似,不同子集间的元素尽量不相似。这些子集又被称为簇(cluster),一般没有交集。
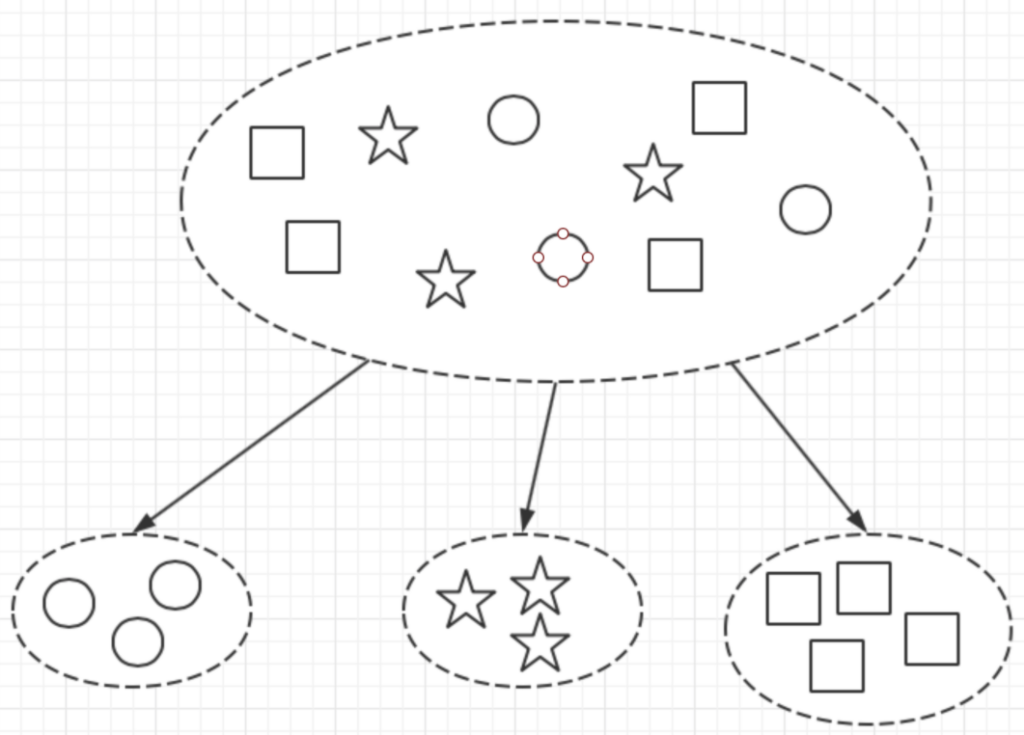
一般将聚类时簇的数量视作由使用者指定的超参数,虽然存在许多自动判断的算法,但它们往往需要人工指定其他超参数。 根据聚类结果的结构,聚类算法也可以分为划分式(partitional )和层次化(hierarchieal两种。划分聚类的结果是一系列不相交的子集,而层次聚类的结果是一棵树, 叶子节点是元素,父节点是簇。本章主要介绍划分聚类。
2. 文本聚类
文本聚类指的是对文档进行聚类分析,被广泛用于文本挖掘和信息检索领域。 文本聚类的基本流程分为特征提取和向量聚类两步, 如果能将文档表示为向量,就可以对其应用聚类算法。这种表示过程称为特征提取,而一旦将文档表示为向量,剩下的算法就与文档无关了。这种抽象思维无论是从软件工程的角度,还是从数学应用的角度都十分简洁有效。
二、文档的特征提取
- 词袋模型 词袋(bag-of-words )是信息检索与自然语言处理中最常用的文档表示模型,它将文档想象为一个装有词语的袋子, 通过袋子中每种词语的计数等统计量将文档表示为向量。比如下面的例子:
人 吃 鱼。
美味 好 吃!统计词频后如下:
人=1
吃=2
鱼=1
美味=1
好=1文档经过该词袋模型得到的向量表示为[1,2,1,1,1],这 5 个维度分别表示这 5 种词语的词频。
一般选取训练集文档的所有词语构成一个词表,词表之外的词语称为 oov,不予考虑。一旦词表固定下来,假设大小为 N。则任何一个文档都可以通过这种方法转换为一个N维向量。词袋模型不考虑词序,也正因为这个原因,词袋模型损失了词序中蕴含的语义,比如,对于词袋模型来讲,“人吃鱼”和“鱼吃人”是一样的,这就不对了。
不过目前工业界已经发展出很好的词向量表示方法了: word2vec/bert 模型等。
- 词袋中的统计指标 词袋模型并非只是选取词频作为统计指标,而是存在许多选项。常见的统计指标如下:
- 布尔词频: 词频非零的话截取为1,否则为0,适合长度较短的数据集
- TF-IDF: 适合主题较少的数据集
- 词向量: 如果词语本身也是某种向量的话,则可以将所有词语的词向量求和作为文档向量。适合处理 OOV 问题严重的数据集。
- 词频向量: 适合主题较多的数据集 定义由 n 个文档组成的集合为 S,定义其中第 i 个文档 di 的特征向量为 di,其公式如下:
$$
d_{i}=\left(\mathrm{TF}\left(t_{1}, d_{i}\right), \mathrm{TF}\left(t_{2}, d_{i}\right), \cdots, \mathrm{TF}\left(t_{j}, d_{i}\right), \cdots, \mathrm{TF}\left(t_{m}, d_{i}\right)\right)
$$
- 其中 $t_j$表示词表中第 j 种单词,m 为词表大小, $TF(t_j, d_i)$ 表示单词 $t_j$ 在文档 $d_i$ 中的出现次数。为了处理长度不同的文档,通常将文档向量处理为单位向量,即缩放向量使得 ||d||=1。
三、k均值算法
一种简单实用的聚类算法是k均值算法(k-means),由Stuart Lloyd于1957年提出。该算法虽然无法保证一定能够得到最优聚类结果,但实践效果非常好。基于k均值算法衍生出许多改进算法,先介绍 k均值算法,然后推导它的一个变种。
1.基本原理
形式化啊定义 k均值算法所解决的问题,给定 n 个向量 $d_1$ 到 $d_n$,以及一个整数 k,要求找出 k 个簇 $S_1$ 到 $S_k$ 以及各自的质心 $C_1$ 到 $C_k$,使得下式最小:
$$
\text { minimize } \mathcal{I}{\text {Euclidean }}=\sum{r=1}^{k} \sum_{d_{i} \in S_{r}}\left|\boldsymbol{d}{i}-\boldsymbol{c}{r}\right|^{2}
$$
其中 $||d_i – c_r||$ 是向量与质心的欧拉距离,I(Euclidean) 称作聚类的准则函数。也就是说,k均值以最小化每个向量到质心的欧拉距离的平方和为准则进行聚类,所以该准则函数有时也称作平方误差和函数。而质心的计算就是簇内数据点的几何平均:
$$
\begin{array}{l}
s_{i}=\sum_{v_{0}} d_{j} \in S_{i} d_{j} \
c_{i}=\frac{s_{i}}{\left|S_{i}\right|} \
\end{array}
$$
其中,$S_i$ 是簇 $S_i$ 内所有向量之和,称作合成向量。
生成 k 个簇的 k均值算法是一种迭代式算法,每次迭代都在上一步的基础上优化聚类结果,步骤如下:
- 选取 k 个点作为 k 个簇的初始质心。
- 将所有点分别分配给最近的质心所在的簇。
- 重新计算每个簇的质心。
- 重复步骤 2 和步骤 3 直到质心不再发生变化。 k均值算法虽然无法保证收敛到全局最优,但能够有效地收敛到一个局部最优点。对于该算法,初级读者重点需要关注两个问题,即初始质心的选取和两点距离的度量。
2.初始质心的选取
由于 k均值不保证收敏到全局最优,所以初始质心的选取对k均值的运行结果影响非常大,如果选取不当,则可能收敛到一个较差的局部最优点。 一种更高效的方法是, 将质心的选取也视作准则函数进行迭代式优化的过程。其具体做法是,先随机选择第一个数据点作为质心,视作只有一个簇计算准则函数。同时维护每个点到最近质心的距离的平方,作为一个映射数组 M。接着,随机取准则函数值的一部分记作。遍历剩下的所有数据点,若该点到最近质心的距离的平方小于0,则选取该点添加到质心列表,同时更新准则函数与 M。如此循环多次,直至凑足 k 个初始质心。这种方法可行的原理在于,每新增一个质心,都保证了准则函数的值下降一个随机比率。 而朴素实现相当于每次新增的质心都是完全随机的,准则函数的增减无法控制。孰优孰劣,一目了然。 考虑到 k均值是一种迭代式的算法, 需要反复计算质心与两点距离,这部分计算通常是效瓶颈。为了改进朴素 k均值算法的运行效率,HanLP利用种更快的准则函数实现了k均值的变种。
3.更快的准则函数
除了欧拉准则函数,还存在一种基于余弦距离的准则函数:
$$
\operatorname{maximize} \mathcal{I}{\cos }=\sum{r=1}^{k} \sum_{d_{i} \in S_{r}} \cos \left(\boldsymbol{d}{i}, \boldsymbol{c}{r}\right)
$$
该函数使用余弦函数衡量点与质心的相似度,目标是最大化同簇内点与质心的相似度。将向量夹角计算公式代人,该准则函数变换为:
$$
\mathcal{I}{\cos }=\sum{r=1}^{k} \sum_{d_{i} \in S_{r}} \frac{d_{i} \cdot c_{r}}{\left|c_{r}\right|}
$$
代入后变换为:
$$
\mathcal{I}{\text {cos }}=\sum{r=1}^{k} \frac{S_{r} \cdot c_{r}}{\left|c_{r}\right|}=\sum_{r=1}^{k} \frac{\left|S_{r}\right| c_{r} \cdot c_{r}}{\left|c_{r}\right|}=\sum_{r=1}^{k}\left|S_{r}\right|\left|c_{r}\right|=\sum_{r=1}^{k}\left|s_{r}\right|
$$
也就是说,余弦准则函数等于 k 个簇各自合成向量的长度之和。比较之前的准则函数会发现在数据点从原簇移动到新簇时,I(Euclidean) 需要重新计算质心,以及两个簇内所有点到新质心的距离。而对于I(cos),由于发生改变的只有原簇和新簇两个合成向量,只需求两者的长度即可,计算量一下子减小不少。
基于新准则函数 $I(cos)$,k均值变种算法流程如下:
- 选取 k 个点作为 k 个簇的初始质心。
- 将所有点分别分配给最近的质心所在的簇。
- 对每个点,计算将其移入另一个簇时 I(cos) 的增大量,找出最大增大量,并完成移动。
- 重复步骤 3 直到达到最大迭代次数,或簇的划分不再变化。
4.实现
在 HanLP 中,聚类算法实现为 ClusterAnalyzer,可以将其想象为一个文档 id 到文档向量的映射容器。 此处以某音乐网站中的用户聚类为案例讲解聚类模块的用法。假设该音乐网站将 6 位用户点播的歌曲的流派记录下来,并且分别拼接为 6 段文本。给定用户名称与这 6 段播放历史,要求将这 6 位用户划分为 3 个簇。实现代码如下:
from pyhanlp import *
ClusterAnalyzer = JClass('com.hankcs.hanlp.mining.cluster.ClusterAnalyzer')
if __name__ == '__main__':
analyzer = ClusterAnalyzer()
analyzer.addDocument("赵一", "流行, 流行, 流行, 流行, 流行, 流行, 流行, 流行, 流行, 流行, 蓝调, 蓝调, 蓝调, 蓝调, 蓝调, 蓝调, 摇滚, 摇滚, 摇滚, 摇滚")
analyzer.addDocument("钱二", "爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲")
analyzer.addDocument("张三", "古典, 古典, 古典, 古典, 民谣, 民谣, 民谣, 民谣")
analyzer.addDocument("李四", "爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 金属, 金属, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲")
analyzer.addDocument("王五", "流行, 流行, 流行, 流行, 摇滚, 摇滚, 摇滚, 嘻哈, 嘻哈, 嘻哈")
analyzer.addDocument("马六", "古典, 古典, 古典, 古典, 古典, 古典, 古典, 古典, 摇滚")
print(analyzer.kmeans(3))结果如下:
[[李四, 钱二], [王五, 赵一], [张三, 马六]]通过 k均值聚类算法,我们成功的将用户按兴趣分组,获得了“人以群分”的效果。
聚类结果中簇的顺序是随机的,每个簇中的元素也是无序的,由于 k均值是个随机算法,有小概率得到不同的结果。
该聚类模块可以接受任意文本作为文档,而不需要用特殊分隔符隔开单词。
四、 重复二分聚类算法
1.基本原理
重复二分聚类(repeated bisection clustering) 是 k均值算法的效率加强版,其名称中的bisection是“二分”的意思,指的是反复对子集进行二分。该算法的步骤如下:
- 挑选一个簇进行划分。
- 利用 k均值算法将该簇划分为 2 个子集。
- 重复步骤 1 和步骤 2,直到产生足够舒朗的簇。 每次产生的簇由上到下形成了一颗二叉树结构。

正是由于这个性质,重复二分聚类算得上一种基于划分的层次聚类算法。如果我们把算法运行的中间结果存储起来,就能输出一棵具有层级关系的树。树上每个节点都是一个簇,父子节点对应的簇满足包含关系。虽然每次划分都基于 k均值,由于每次二分都仅仅在一个子集上进行,输人数据少,算法自然更快。
在步骤1中,HanLP采用二分后准则函数的增幅最大为策略,每产生一个新簇,都试着将其二分并计算准则函数的增幅。然后对增幅最大的簇执行二分,重复多次直到满足算法停止条件。
2.自动判断聚类个数k
聚类个数 k 这个超参数很难准确估计。在重复二分聚类算法中,有一种变通的方法,那就是通过给准则函数的增幅设定阈值 β 来自动判断 k。此时算法的停止条件为,当一个簇的二分增幅小于 β 时不再对该簇进行划分,即认为这个簇已经达到最终状态,不可再分。当所有簇都不可再分时,算法终止,最终产生的聚类数量就不再需要人工指定了。
3.实现
from pyhanlp import *
ClusterAnalyzer = JClass('com.hankcs.hanlp.mining.cluster.ClusterAnalyzer')
if __name__ == '__main__':
analyzer = ClusterAnalyzer()
analyzer.addDocument("赵一", "流行, 流行, 流行, 流行, 流行, 流行, 流行, 流行, 流行, 流行, 蓝调, 蓝调, 蓝调, 蓝调, 蓝调, 蓝调, 摇滚, 摇滚, 摇滚, 摇滚")
analyzer.addDocument("钱二", "爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲")
analyzer.addDocument("张三", "古典, 古典, 古典, 古典, 民谣, 民谣, 民谣, 民谣")
analyzer.addDocument("李四", "爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 金属, 金属, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲")
analyzer.addDocument("王五", "流行, 流行, 流行, 流行, 摇滚, 摇滚, 摇滚, 嘻哈, 嘻哈, 嘻哈")
analyzer.addDocument("马六", "古典, 古典, 古典, 古典, 古典, 古典, 古典, 古典, 摇滚")
print(analyzer.repeatedBisection(3)) # 重复二分聚类
print(analyzer.repeatedBisection(1.0)) # 自动判断聚类数量k运行结果如下:
[[李四, 钱二], [王五, 赵一], [张三, 马六]]
[[李四, 钱二], [王五, 赵一], [张三, 马六]]与上面音乐案例得出的结果一致,但运行速度要快不少。
