测验的项目分析
一、测验项目的难度
- 二分法记分项目的难度
- 通过率
不考虑作答是否源于猜测的概率,二分法记分的测验项目常用通过率表示,即:$P=\frac{R}{N}$,其中$P, R, N$分别代表项目难度,答对或通过的人数,全体被试数。 - 极端分组法
被试人数较多,可将被试者按照总分分组,总分最高的27%为被试高分组($N_{H}$),总分最低的27%为被试低分组($N_{L}$),分别计算高分和低分组的通过率,然后求项目难度,通过率$P=\frac{P_{H}+P_{L}}{2}$。$P_{H}, P_{L}$分别代表高、低分组的通过率。
- 通过率
- 非二分法记分项目的难度
$P=\frac{\bar{x}}{x_{\max }}$, $\bar{x}$代表某项目的平均分, ,$x_{\max }$代表该项目满分。
难度的等距变换
通过率仅是题目的相对难度,无法进一步计算比较,需转换成等距量表。例:测验题目难易转换
$Z$分数有小数点和负值,为了表示方便,常用美国教育测验服务中心采用的难度指标:$\Delta=13+4 \cdot Z$。 根据统计$3 \sigma$原则,标准正态分布的$Z$一般在-3到+3之间,所以等距难度指数$\Delta$上限为25,下限为1,平均数为13,标准差为4,$\Delta$越高,难度越大。
二、测验项目的区分度
- 鉴别指数:
$D=P_{H}-P_{L}$
从分数分布两端各选择27%(27%为标准测试采用的常用惯例,一般情况下介于25%-33%之间,测试人数少于100人则不宜采用27%规则,而用50%作为分界点。)分为高、低分组分别计算通过率,两数之差就是鉴别指数。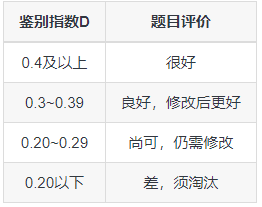
$D$缺点:该统计量无样本分布,无法进行统计处理。无法回答如“两个箱项目D值差异达到多少才具有显著差异”等问题。 - 相关法
用项目分数与总分的相关作为项目区分度指标,相关越高,项目区分度就越高。- 点二列相关
适用于0、1记分(或二分变量),测验总分是连续变量的情况,计算结果需进行显著性检验,计算公式:
$$r_{pb}=\frac{\bar x_p-\bar x_q}{S_t} \sqrt{pq}$$
其中,$\bar x_p$为通过该项目被试的平均分数,$\bar x_q$为未通过该项目被试的平均分数, $p$为通过该项目的被试人数百分比,$q$为未通过该项目的被试人数百分比, $S_t$为全体被试的分数标准差。例:点二列相关计算 - 二列相关
dnorm(qnorm(pass))
适用于连续变量,但其中一个变量被认为地分成两类。例如,当一个测验项目分数是连续的,但是总分被分为高、低或及格、不及格两类时。计算公式为:
$$r_{b}=\frac{\bar x_p-\bar x_q}{S_t} \cdot \frac{pq}{y}$$
其中$y$为正态分布下p的高度(R语言dnorm(qnorm(p))),其余同上。
二列相关系数显著性可用下公式检验:
$$Z=\frac{r_b}{\frac{1}{y} \sqrt{\frac{pq}{N}}}$$
其中$N$为被试总人数,其余同上。 - $\varphi$相关
适用于两个变量都是二分名义变量,也可用与连续变量,$\varphi$相关不要求变量呈正态分布,所求指标为 $\varphi$系数。例:$\varphi$系数计算
$$r_{\varphi}=\frac{a d-b c}{\sqrt{(a+b)(a+c)(b+d)(c+d)}}$$
$\varphi$相关的显著性可以进行$\chi^{2}$检验。
$$\chi^{2}=N \cdot r_{\varphi}^{2}$$
- 点二列相关
三、项目难度的校正
客观题由于猜测本身引起误差,所以对于某些测验项目,猜测会影响项目难度的变化,因此在作项目难度比较时有必要对猜测进行校正。
选择题测验中,猜测成功的概率$P$受备选答案数$K$的影响, 备选答案数目少 ,机遇作用越大。根据难度计算公式不能反应项目真实难度,可用下式对难度校正:
$$CP=\frac{K P-1}{K-1}$$
其中,$CP$校正后的通过率,$P$为实际通过率,$K$为备选答案数目。
对被试者得分进行校正:
$$S=R-\frac{W}{K-1}$$
其中$S$为校正后的得分,$R$为被试者答对的项目数,$W$为被试者答错的项目数,$K$为项目的选项数目。
