- 积差相关,又称为皮尔逊相关。使用要求:成对数据,等距或等比性质的两连续变量,正态分布,样本数量大于30。例如每个学生的智力和学习成绩,每个人的身高和体重等。任意两个个体之间不能求皮尔逊相关。
- 斯皮尔曼等级相关。积差相关的延申,精度小于积差相关。使用要求:成对数据,等距或等比性质的两连续变量,数据分布无要求,样本数可小于30。
- 肯德尔等级相关。用字母$W$表示,又称为肯德尔和谐系数,功用与斯皮尔曼等级相关相同,适合于两列以上的等级变量。
一、积差相关
$$r = \frac {\sum xy}{Ns_Xs_Y}$$
式中:
$x,y$为两变量离均差, $x = X – \overline X$ $Y = Y- \overline Y$
$N$为成对数据的数目,
$s_X$为$X$变量的标准差, $s_Y$为$Y$变量的标准差
例1:两学科成绩相关性(皮尔逊相关)
某班50名学生学生某次测验成绩如下,问两科目成绩是否具有一致性。
set.seed(1)
x <- round(runif(50,40,100))
set.seed(2)
y <- round(runif(50,40,100))
N <- 50
m_x <- x - mean(x)
m_y <- y - mean(y)
sx <- sd(x)
sy <- sd(y)
r1 <- sum(m_x*m_y)/(N*sx*sy) # 0.146
# cor()直接计算
r2 <-cor(x,y,method = "pearson") # 0.149二、斯皮尔曼等级相关
$$r_R =1- \frac {6{\sum D^2}}{N(N^2-1)}$$
式中:
$N$为等级个数, $D$指二列成对变量的等级差数 。
例1:两学科成绩相关性(斯皮尔曼相关)
某班10名学生某次测验成绩如下,问两科目成绩是否具有一致性。

set.seed(1)
x <- round(runif(10,40,100))
set.seed(2)
y <- round(runif(10,40,100))
N <- 10
D <- rank(x)-rank(y)
r1 <- 1-(6*sum(D^2))/(N*(N^2-1)) # -0.281
# cor()直接计算
r2 <- cor(x,y,method = "spearman") # -0.289例2:视听反映是否一致
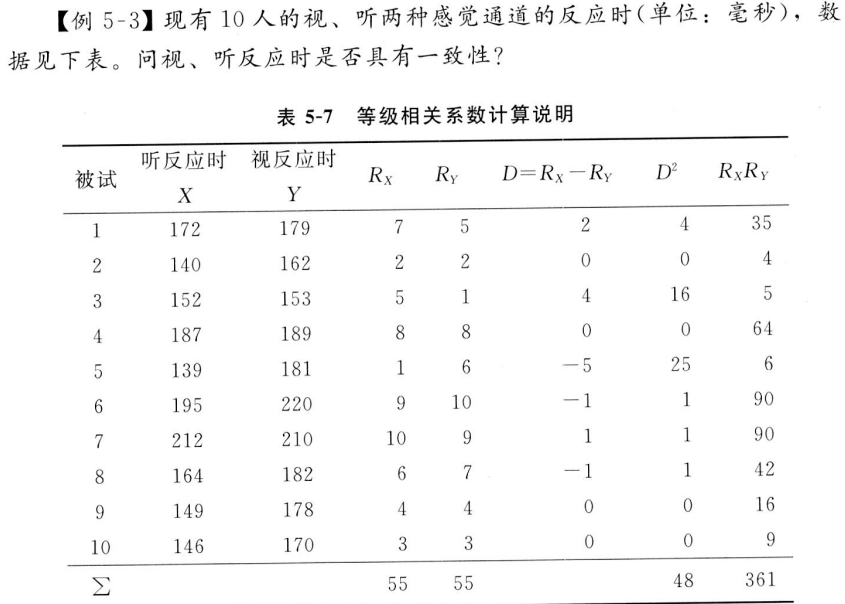
N <- 10
x <- c(172,140,152,187,139,195,212,164,149,146)
y <- c(179,162,153,189,181,220,210,182,178,170)
D <- rank(x)-rank(y)
r1 <- 1-(6*sum(D^2))/(N*(N^2-1)) # 0.7090909
# cor()直接计算
r2 <- cor(x,y,method = "spearman") # 0.7090909三、肯德尔等级相关
同一评价者无相同等级评定时,W的计算公式:
$$W = \frac {s}{ \frac {1}{12}K^2(N^3-N)}$$
式中:
$s=\sum(R_i-\frac{\sum R_i}{N})^2$;
$R_i代$表评价对象获得的K个等级之和;
$K$代表等级评定者数;
$N$代表被等级评定的对象数目。
同一评价者有相同等级评定时,W的计算公式:
$$W = \frac {s}{ \frac {1}{12}K^2(N^3-N)-K \sum T}$$
其中:
$\sum T = \sum\frac{n_{ij}^3-n_{ij}}{12}$,$n_{ij}$为第$i$个评价者的评定结果中第$j$个重复等级的相同等级数。
$W$介于0到1之间,W=1表示K个评价者意见完全一致,0<W<1代表K个评价者意见存在一定关系,但不完全一致,W=0表示K个评价者意见完全不一致。
例1:作文评分标准掌握是否一致
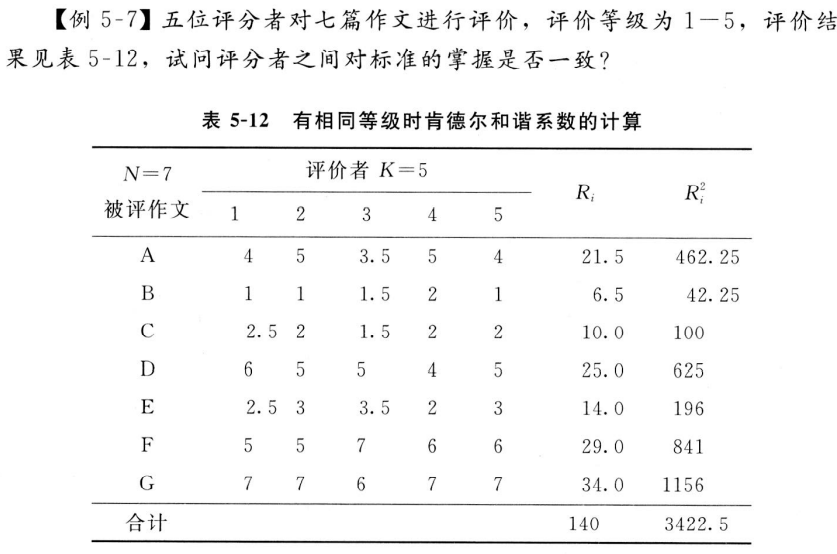
data <- data.frame(K1 = c(4,1,2.5,6,2.5,5,7),
K2 = c(5,1,2,5,3,5,7),
K3 = c(3.5,1.5,1.5,5,3.5,7,6),
K4 = c(5,2,2,4,2,6,7),
K5 = c(4,1,2,5,3,6,7)
)
rownames(data) <- LETTERS[1:7]
N <- 7
K <- 5
R_i <- rowSums(sapply(data, rank))
s <- sum( (R_i-sum(R_i)/N)^2 )
# T_ij计算
T_ij <- function(x){
tmp <- table(x)
n <- tmp[tmp >= 2]
T_ij <- (n^3-n)/12
return(as.numeric(T_ij))
}
T_ij_sum <- sum(unlist(sapply(data,T_ij))) # 5.5
W <- s/(K^2*(N^3-N)/12-K*T_ij_sum) # 0.9256
# 五位评分这对七篇作文的评价标准比较一致例2:对颜色喜爱程度是否一致
假设有10人对7种颜色的喜爱程度进行评级,最喜欢为7,最不喜欢为1,结果如下表,问这10人对颜色的爱好是否一致。
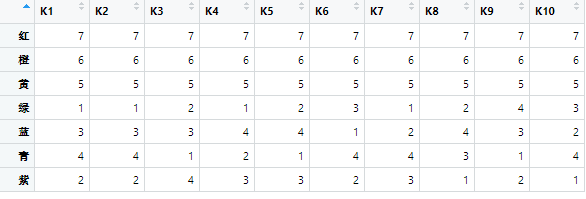
# 下数据模拟10人对"红","橙","黄"喜爱程度一致,计算W结果为0.84
set.seed(1)
data <- data.frame(K1 = c(7,6,5,sample(1:4,4)),
K2 = c(7,6,5,sample(1:4,4)),
K3 = c(7,6,5,sample(1:4,4)),
K4 = c(7,6,5,sample(1:4,4)),
K5 = c(7,6,5,sample(1:4,4)),
K6 = c(7,6,5,sample(1:4,4)),
K7 = c(7,6,5,sample(1:4,4)),
K8 = c(7,6,5,sample(1:4,4)),
K9 = c(7,6,5,sample(1:4,4)),
K10 = c(7,6,5,sample(1:4,4))
)
rownames(data) <- c("红","橙","黄","绿","蓝","青","紫")
# 下数据模拟10人对所有颜色喜爱程度一致,计算W结果为1
# data <- data.frame(K1 = 7:1,
# K2 = 7:1,
# K3 = 7:1,
# K4 = 7:1,
# K5 = 7:1,
# K6 = 7:1,
# K7 = 7:1,
# K8 = 7:1,
# K9 = 7:1,
# K10 = 7:1
# )
#
# rownames(data) <- c("红","橙","黄","绿","蓝","青","紫")
N <- 7
K <- 10
R_i <- rowSums(sapply(data, rank))
s <- sum( (R_i-sum(R_i)/N)^2 )
# T_ij计算计算
T_ij <- function(x){
tmp <- table(x)
n <- tmp[tmp >= 2]
T_ij <- (n^3-n)/12
return(as.numeric(T_ij))
}
T_ij_sum <- sum(unlist(sapply(data,T_ij))) # 结果为0 (同一评价者无相同等级评定)
W <- s/(K^2*(N^3-N)/12-K*T_ij_sum) # 0.84
# 从W值看,这10个人对颜色喜爱具有较高一致性
