矩阵微积分
虽然前面章节中的主题通常包含在线性代数的标准课程中,但似乎很少涉及(我们将广泛使用)的一个主题是微积分扩展到向量设置展。尽管我们使用的所有实际微积分都是相对微不足道的,但是符号通常会使事情看起来比实际困难得多。 在本节中,我们将介绍矩阵微积分的一些基本定义,并提供一些示例。
1. 梯度
假设$f: \mathbb{R}^{m \times n} \rightarrow \mathbb{R}$是将维度为$m \times n$的矩阵$A\in \mathbb{R}^{m \times n}$作为输入并返回实数值的函数。 然后$f$的梯度(相对于$A\in \mathbb{R}^{m \times n}$)是偏导数矩阵,定义如下:
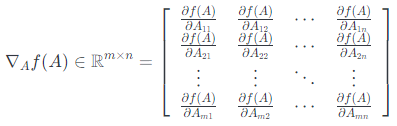
即,$m \times n$矩阵:
$$\left(\nabla_{A} f(A)\right)_{i j}=\frac{\partial f(A)}{\partial A{i j}}$$
请注意,$\nabla_{A} f(A) $的维度始终与$A$的维度相同。特殊情况,如果$A$只是向量$A\in \mathbb{R}^{n}$,则
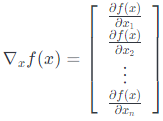
重要的是要记住,只有当函数是实值时,即如果函数返回标量值,才定义函数的梯度。例如,$A\in \mathbb{R}^{m \times n}$相对于$x$,我们不能取$Ax$的梯度,因为这个量是向量值。
它直接从偏导数的等价性质得出:
- $\nabla_{x}(f(x)+g(x))=\nabla_{x} f(x)+\nabla_{x} g(x)$
- 对于$t \in \mathbb{R}$ ,$\nabla_{x}(t f(x))=t \nabla_{x} f(x)$
原则上,梯度是偏导数对多变量函数的自然延伸。然而,在实践中,由于符号的原因,使用梯度有时是很困难的。例如,假设$A\in \mathbb{R}^{m \times n}$是一个固定系数矩阵,假设$b\in \mathbb{R}^{m}$是一个固定系数向量。设$f: \mathbb{R}^{m \times n} \rightarrow \mathbb{R}$为$f(z)=z^Tz$定义的函数,因此$\nabla_{z}f(z)=2z$。但现在考虑表达式,
$$\nabla f(Ax)$$
该表达式应该如何解释? 至少有两种可能性:
1.在第一个解释中,回想起$\nabla_{z}f(z)=2z$。 在这里,我们将$\nabla f(Ax)$解释为评估点$Ax$处的梯度,因此:
$$\nabla f(A x)=2(A x)=2 A x \in \mathbb{R}^{m}$$
2.在第二种解释中,我们将数量$f(Ax)$视为输入变量$x$的函数。 更正式地说,设$g(x) =f(Ax)$。 然后在这个解释中:
$$\nabla f(A x)=\nabla_{x} g(x) \in \mathbb{R}^{n}$$
在这里,我们可以看到这两种解释确实不同。 一种解释产生$m$维向量作为结果,而另一种解释产生$n$维向量作为结果! 我们怎么解决这个问题?
这里,关键是要明确我们要区分的变量。
在第一种情况下,我们将函数$f$与其参数$z$进行区分,然后替换参数$Ax$。
在第二种情况下,我们将复合函数$g(x)=f(Ax)$直接与$x$进行微分。
我们将第一种情况表示为$\nabla zf(Ax)$,第二种情况表示为$\nabla xf(Ax)$。
2. 黑塞矩阵
假设$f: \mathbb{R}^{n} \rightarrow \mathbb{R}$是一个函数,它接受$\mathbb{R}^{n}$中的向量并返回实数。那么关于$x$的黑塞矩阵(也有翻译作海森矩阵),写做:$\nabla_x ^2 f(A x)$,或者简单地说,$H$是$n \times n$矩阵的偏导数:
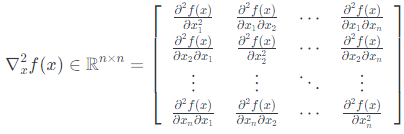
换句话说,$\nabla_{x}^{2} f(x) \in \mathbb{R}^{n \times n}$,其:
$$\left(\nabla_{x}^{2} f(x)\right)_{i j}=\frac{\partial^{2} f(x)}{\partial x{i} \partial x_{j}}$$
注意:黑塞矩阵通常是对称阵:
$$\frac{\partial^{2} f(x)}{\partial x_{i} \partial x_{j}}=\frac{\partial^{2} f(x)}{\partial x_{j} \partial x_{i}}$$
与梯度相似,只有当$f(x)$为实值时才定义黑塞矩阵。
很自然地认为梯度与向量函数的一阶导数的相似,而黑塞矩阵与二阶导数的相似(我们使用的符号也暗示了这种关系)。 这种直觉通常是正确的,但需要记住以下几个注意事项。
首先,对于一个变量$f: \mathbb{R} \rightarrow \mathbb{R}$的实值函数,它的基本定义:二阶导数是一阶导数的导数,即:
$$\frac{\partial^{2} f(x)}{\partial x^{2}}=\frac{\partial}{\partial x} \frac{\partial}{\partial x} f(x)$$
然而,对于向量的函数,函数的梯度是一个向量,我们不能取向量的梯度,即:
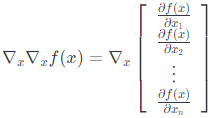
上面这个表达式没有意义。 因此,黑塞矩阵不是梯度的梯度。 然而,下面这种情况却这几乎是正确的:如果我们看一下梯度$\left(\nabla_{x} f(x)\right)_{i}=\partial f(x) / \partial x{i}$的第$i$个元素,并取关于于$x$的梯度我们得到:
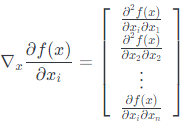
这是黑塞矩阵第$i$行(列),所以:
$$\nabla_{x}^{2} f(x)=\left[\nabla_{x}\left(\nabla_{x} f(x)\right)_{1} \quad \nabla{x}\left(\nabla_{x} f(x)\right)_{2} \quad \cdots \quad \nabla{x}\left(\nabla_{x} f(x)\right)_{n}\right]$$
简单地说:我们可以说由于:$\nabla_{x}^{2} f(x)=\nabla_{x}\left(\nabla_{x} f(x)\right)^{T}$,只要我们理解,这实际上是取$\nabla_{x} f(x)$的每个元素的梯度,而不是整个向量的梯度。
最后,请注意,虽然我们可以对矩阵$A\in \mathbb{R}^{n}$取梯度,但对于一般的机器学习,只考虑对向量$x \in \mathbb{R}^{n}$取黑塞矩阵。
这会方便很多(事实上,我们所做的任何计算都不要求我们找到关于矩阵的黑森方程),因为关于矩阵的黑塞方程就必须对矩阵所有元素求偏导数$\partial^{2} f(A) /\left(\partial A_{i j} \partial A_{k \ell}\right)$,将其表示为矩阵相当麻烦。
3. 二次函数和线性函数的梯度和黑塞矩阵
尝试几个简单函数的梯度和黑塞矩阵:
对于$x \in \mathbb{R}^{n}$, 设$f(x)=b^Tx$ 的某些已知向量$b \in \mathbb{R}^{n}$ ,则:
$$f(x)=\sum_{i=1}^{n} b_{i} x_{i}$$
所以:
$$\frac{\partial f(x)}{\partial x_{k}}=\frac{\partial}{\partial x_{k}} \sum_{i=1}^{n} b_{i} x_{i}=b_{k}$$
由此我们可以很容易地看出$\nabla_{x} b^{T} x=b$。 这应该与单变量微积分中的类似情况进行比较,其中$\partial /(\partial x) a x=a$。
现在考虑$A\in \mathbb{S}^{n}$的二次函数$f(x)=x^TAx$。 记住这一点:
$$f(x)=\sum_{i=1}^{n} \sum_{j=1}^{n} A_{i j} x_{i} x_{j}$$
为了取偏导数,我们将分别考虑包括$x_k$和$x_2^k$因子的项:
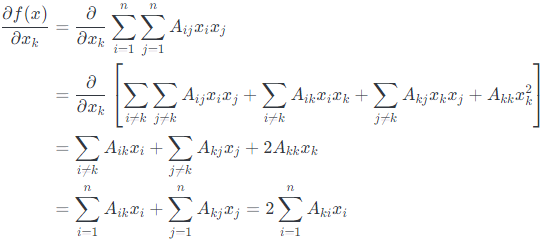
最后一个等式,是因为$A$是对称的(我们可以安全地假设,因为它以二次形式出现)。 注意,$\nabla_{x} f(x)$的第$k$个元素是$A$和$x$的第$k$行的内积。 因此,$\nabla_{x} x^{T} A x=2 A x$。 同样,这应该提醒你单变量微积分中的类似事实,即$\partial /(\partial x) a x^{2}=2 a x$。
最后,让我们来看看二次函数$f(x)=x^TAx$黑塞矩阵(显然,线性函数$b^Tx$的黑塞矩阵为零)。在这种情况下:
$$\frac{\partial^{2} f(x)}{\partial x_{k} \partial x_{\ell}}=\frac{\partial}{\partial x_{k}}\left[\frac{\partial f(x)}{\partial x_{\ell}}\right]=\frac{\partial}{\partial x_{k}}\left[2 \sum_{i=1}^{n} A_{\ell i} x_{i}\right]=2 A_{\ell k}=2 A_{k \ell}$$
因此,应该很清楚$\nabla_{x}^2 x^{T} A x=2 A$,这应该是完全可以理解的(同样类似于$\partial^2 /(\partial x^2) a x^{2}=2a$的单变量事实)。
简要概括起来:
- $\nabla_{x} b^{T} x=b$
- $\nabla_{x} x^{T} A x=2 A x$ (如果$A$是对称阵)
- $\nabla_{x}^2 x^{T} A x=2 A $ (如果$A$是对称阵)
4. 最小二乘法
让我们应用上一节中得到的方程来推导最小二乘方程。假设我们得到矩阵$A\in \mathbb{R}^{m \times n}$(为了简单起见,我们假设$A$是满秩)和向量$b\in \mathbb{R}^{m}$,从而使$b \notin \mathcal{R}(A)$。在这种情况下,我们将无法找到向量$x\in \mathbb{R}^{n}$,由于$Ax = b$,因此我们想要找到一个向量$x$,使得$Ax$尽可能接近 $b$,用欧几里德范数的平方$|A x-b|_{2}^{2} $来衡量。
使用公式$|x|^{2}=x^Tx$,我们可以得到:
$$\begin{aligned}|A x-b|_{2}^{2} &=(A x-b)^{T}(A x-b) \ &=x^{T} A^{T} A x-2 b^{T} A x+b^{T} b \end{aligned}$$
根据$x$的梯度,并利用上一节中推导的性质:
$$\begin{aligned} \nabla_{x}\left(x^{T} A^{T} A x-2 b^{T} A x+b^{T} b\right) &=\nabla_{x} x^{T} A^{T} A x-\nabla_{x} 2 b^{T} A x+\nabla_{x} b^{T} b \\ &=2 A^{T} A x-2 A^{T} b \end{aligned}$$
将最后一个表达式设置为零,然后解出$x$,得到了正规方程:
$$x = (A^TA)^{-1}A^Tb$$
